4 Käytännön todennäköisyysjakaumia (lisää)
Viimeistään tilastotieteiden perusteissa tutuksi tulleen normaalijakauman asema useissa käytännön sovelluksissa on tärkeä. Tämä johtuu lähinnä normaalijakauman teoreettisista ominaisuuksista - erityisesti seuraavasta: kun summataan paljon monenlaisia satunnaismuuttujia yhteen ja lasketaan niiden summa, niin tämä lähestyy normaalijakaumaa. Käytännön elämässä monet havaitut suureet ovat monitekijäisiä ja kun näitä satunnaisia muita tekijöitä on paljon, niin havaintoaineisto alkaa helposti näyttämään normaalijakaumalta. Klassisena esimerkkinä vaikkapa ihmisten pituuden jakauma populaatiossa: ihmisen pituuteen vaikuttaa hyvin monet erilaiset satunnaiset tekijät (tekijöitä on arveltu olevan useampi sata), ja tämän takia pituuksien jakaumat näyttävätkin hyvin usein normaalisilta. Normaalijakauma tulee vastaan myös tilanteissa, joissa varsinainen kiinnostava ilmiö on yksitekijäinen, mutta havaittuihin suureisiin vaikuttaa suuri joukko satunnaisia virhetekijöitä.
Jos sen sijaan pyritään kuvaamaan havaintojen sijaan enemmän varsinaisen kiinnostavan ilmiön satunnaisuutta, niin normaalijakauma ei välttämättä ole enää ensimmäinen vaihtoehto. Tässä kappaleessa tutustutaan muutamaan paljon käytettyyn todennäköisyysjakaumaan, joilla on oma vankka asemansa tietyissä käytännön sovelluksissa.
4.1 Eksponenttijakauma
Jatkuvan satunnaismuuttujan \(X\) sanotaan olevan eksponentiaalisesti jakautunut parametrilla \(\lambda >0\), jos sen tiheysfunktio (tf) on \[ f(x;\lambda) = \begin{cases} \lambda e^{-\lambda x}& \text{kun } x\geq 0 &\\ 0& \text{muulloin} \end{cases}.\]
Merkintä eksponenttijakautuneelle satunnaismuuttujalle \(X\) on \(X\sim Exp(\lambda)\). Yllä olevassa tiheysfunktion muodossa parametriä \(\lambda\) kutsutaan usein ‘rate’-parametriksi (tai vauhtiparametriksi). Eksponenttijakauma parametrisoidaan joskus myös em. rate-parametrin käänteisluvun suhteen, jolloin tiheysfunktio on muotoa \[f(x;\mu)=\frac{e^{- x/\mu}}{\mu},\] ja jolloin parametriä \(\mu\) kutsutaan usein ‘scale’ parametriksi (tai skaalaparametriksi). Tässä materiaalissa eksponenttijakaumalle käytetään kuitenkin primääristi ensimmäistä muotoa.
4.1.1 Eksponenttijakauman ominaisuuksia
Satunnaismuuttujalle \(X\sim Exp(\lambda)\) on voimassa
- Satunnaismuuttujan tiheysfunktio \(\lambda e^{-\lambda x}\) on muuttujan suhteen vähenevä funktio, ja vähenemisvauhti riippuu parametrin \(\lambda\) arvosta.
- Odotusarvo: \(E(X)=\frac{1}{\lambda}\)
- Varianssi: \(Var(X)=\frac{1}{\lambda ^2}\)
- Eksponenttijakauman kertymäfunktio: \[F(x;\lambda)= 1-e^{-\lambda x}, \text{ kun } \lambda >0 \text{ ja } x \geq 0 \]
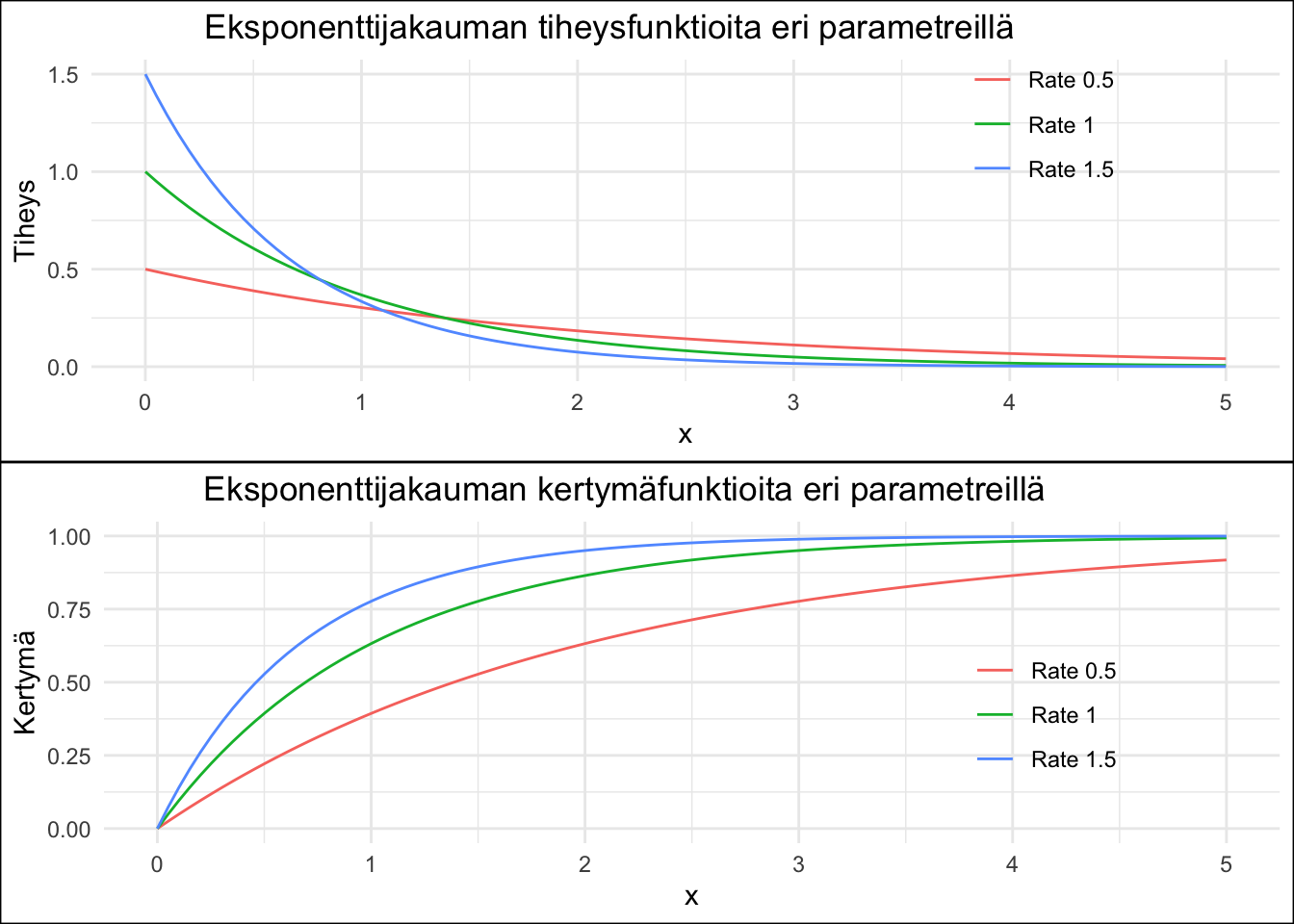
Figure 4.1: Eksponenttijakauman tiheys- ja kertymäfunktiot kolmella eri parametrillä.
Esimerkki 4.1.1.1 (eksponenttijakauman kertymäfunktion lasku)
Soveltamalla kertymäfunktion määritelmää eksponenttijakauman tiheysfunktioon saadaan
\(F(x;\lambda)=\int_{-\infty}^x f(x)dx=\int_{-\infty}^{x}
\lambda e^{-\lambda x}dx\). Kun toisaalta tiedetään, että
satunnaismuuttujan mahdollinen arvoalue on \(x \geq 0\), niin
eksponenttijakauman kertymäfunktion lauseke voidaan kirjoittaa muotoon
\(F(x;\lambda)=\int_{0}^{x} \lambda e^{-\lambda x}dx\). Toisaalta
integraalilaskennan perusteista tiedetään, että \(\int e^{-\lambda
x}dx=-\frac{1}{\lambda}e^{-\lambda x}\) ja siis \(\int \lambda
e^{-\lambda x}dx=-e^{-\lambda x}\). Kysytty integraali voidaan nyt
kirjoittaa muotoon \(F(x;\lambda)=-e^{-\lambda x}+e^{-\lambda
0}=-e^{-\lambda x}+1=1-e^{-\lambda x}.\)
4.1.2 Eksponenttijakauman unohdusominaisuus aka muistinmenetysominaisuus
Kun oletetaan, että \(X \sim Exp(\lambda)\), ja \(a, b \geq 0\) niin tällöin on ehdolliselle todennäköisyydelle on voimassa \[P(X\geq a+b |X\geq a)=P(X\geq b) \text{ (muistinmenetysominaisuus). }\]
Selkokielisemmin: jos oletetaan, että odotusaika on eksponentiaalisesti jakautunut. Tällöin se, että tapahtuman sattumista on odotettu jo ajan \(a\) verran ei vaikuta todennäköisyyteen joutua odottamaan vielä \(b\):n verran lisää. Lyhyesti: odotushistoria ei vaikuta tulevaan.
Tätä laskuja helpottavaa mutta suhteellisen harvinaista matemaattista ominaisuutta kutsutaan muistinmenetysominaisuudeksi tai unohdusominaisuudeksi, jota stokastisten prosessien teoriassa kutsutaan Markov-ominaisuudeksi. Eksponenttijakauman tapauksessa tämän unohdusominaisuuden osoittaminen suoralla laskulla on yksinkertaista.
4.1.3 Eksponenttijakauman sovellusalueita
Eksponenttijakaumaa käytetään erityisesti kuvaamaan odotus- tai jonotusaikoja tapahtumien välillä tai ennen ensimmäistä tapahtumaa, kun
Tapahtumat ovat riippumattomia ja esimerkiksi tapahtuman sattuminen tai sattumattomuus ei vaikuta seuraavan tapahtuman sattumiseen
Tietyllä aikavälillä sattuvien tapahtumien lukumäärä riippuu vain välin pituudesta
Tapahtumat eivät voi sattua samanaikaisesti
Tarkkaan ottaen nämä ehdot ovat reunaehtoja ns. Poisson-prosessille, mutta tämän prosessin ehtoja voidaan käyttää taustaoletuksina useimmissa eksponentiaaliseen jakauman käytännön elämän sovelluksissa.
Tyypillisiä sovellusalueita, joissa käytetään eksponenttijakaumaa on mm.
- Jonoteoria: palvelupyyntöjen (esim. puhelut) väliajat, joissa tietyllä aikavälillä pyyntöjen tapahtumisvauhti on vakio
- Luotettavuusanalyysi: vikaantumisennusteet yksittäisille riippumattomille laitteille tai muille agenteille
- Luottoriskien analyysi: maksuviivästyksien mallinnus
- Vedonlyönti: aika ennen päätetapahtumaa (esim. ensimmäistä maalia)
Näiden tyyppiesimerkkien lisäksi eksponenttijakaumaoletusta käytetään hyvin paljon myös muissa sovelluksissa esimerkiksi katastrofiennusteissa ja epidemiologiassa, jossa odotusaikaa ennen päätetapahtumaa voidaan mallintaa eksponenttijakaumalla.
Pelkästään nämä suuret yläotsikot sisältävät valtavan määrän erilaisia käytännön sovelluksia ja eksponenttijakaumaa voidaan pitää perustellusti yhtenä tärkeimmistä todennäköisyysjakaumista käytännön tilastollisessa mallinnuksessa. Tarkempia kuvauksia eksponenttijakauman sovelluksista löytyy esimerkiksi täältä.
4.1.4 Todennäköisyyksien lasku eksponenttijakaumasta
Eksponenttijakauman todennäköisyydet saadaan helposti edellä mainitusta eksponenttijakauman hyvin yksinkertaista muotoa olevasta kertymäfunktiosta \(P(X \leq x)=F(x;\lambda)= 1-e^{-\lambda x}\) ja tarvittaessa soveltaen normaaleja todennäköisyyslaskennan peruslaskusääntöjä. R:ssä relevantit valmisfunktiot ovat
dexp(x, rate): kertoo tiheysfunktion arvon kohdassa \(x\)pexp(x, rate): kertoo kertymäfunktion arvon kohdassa \(x\)qexp(p,rate): kertoo kertymäfunktion käänteisfunktion arvon todennäköisyydelle \(p\)
Esimerkki 4.1.4.1
Oletetaan, että \(t \sim Exp(2)\). Laske \(P(t\leq 1.5)\).
Ratkaisu
Käytetään eksponenttijakauman kertymäfunktiota \(P(X \leq
x)=F(x;λ)=1−e^{−λx}\), jolloin saadaan \(P(T≤1.5)=1−e^{-2\cdot 1.5}=0.950\).
Sama ratkaisu saadaan R:llä myös suoraan pexp(1.5,rate=2)
Esimerkki 4.1.4.2
Oletetaan, että \(t \sim Exp(4)\). Laske \(P(3 \leq t\leq 5)\).
Ratkaisu
Käytetään eksponenttijakaman kertymäfunktiota \(P(X
\leq x)=F(x;λ)=1−e^{−λx}\) ja tehtävässä annettua parametriä
\(\lambda=4\), jolloin saadaan \(P(3 \leq t \leq 5)=
F(5;4)-F(3;4)\). Käyttämällä eksponenttifunktion tunnettua kertymäfunktiota lukuarvoksi saadaan \((1−e^{−4\cdot 5})-(1−e^{−4\cdot 3}) =1- e^{−20} + e^{-12} - 1=e^{-12}- e^{-20} = 6.142151e-06\).
Sama ratkaisu saadaan R:llä myös suoraan pexp(5,rate=4)-pexp(3,rate=4).
Esimerkki 4.1.4.3
Yritys miettii konserni miettii kustannuslaskelmia varten sopivia
turvamarginaaleja odotusajoilleen, jotka oletetaan eksponentiaalisesti
jakautuneiksi parametrillä \(\lambda=1/45.13\). Laske odotusajalle raja
\(t_0\), jolle yritys pystyy lupaamaan, että vain 5% odotusajoista on
tätä suurempia.
Ratkaisu
Tehtävänannon mukaan halutaan siis
selvittää sellainen \(t_0\), jolle \(P(T \leq t_0)=0.95\). Käyttämällä
eksponenttijakauman kertymäfunktiota saadaan yhtälö \(\left( 1−e^{
-\frac{t_0}{45.13} }\right)=0.95\). Tästä yhtälöstä saadaan edelleen
\(e^{ -\frac{t_0}{45.13} }=1-0.95\). Edelleen ottamalla \(e\)-kantaiset
logaritmit kummaltakin puolelta saadaan
\(-\frac{t_0}{45.13}=ln(0.05)\), josta saadaan ratkaisu
\(t_0=-45.14\cdot ln(0.05)=135.197\).
Sama ratkaisu saadaan R:llä myös suoraan: qexp(0.95,rate=1/45.13).
Esimerkki 4.1.4.4
Anna on ottanut tehtäväkseen varata leffaliput kaveriporukalle, ja liput tulisi
varata ennen klo 18.00, jotta he saavat liput aiottuun näytökseen.
Kaveriporukan Vilmalla oli leffalippujen sarjanumerot, joita Anna kysyi
Vilmalta WhatsAppin kautta klo 17.30. Kello on 17.40 eikä Anna ole vielä
saanut vastausta Vilmalta. Millä todennäköisyydellä Anna saa varattua
leffaliput toivottuun näytökseen, kun tiedetään Vilman vastaavan
keskimäärin puolen tunnin viiveellä ja vastauksen odotusajan olevan
eksponentiaalisesti jakautunut?
Ratkaisu
Tehtävän tietojen keskimääräinen odotusaika (eli odotusarvo) oli tehtävän tietojen mukaan puoli tuntia eli 30 minuuttia, joten eksponenttijakauman parametri (\(\lambda\)) on \(1/30\). Näin ollen \(X \sim Exp(1/30)\).
Laskettava todennäköisyys on nyt \(P(X< 30 |X\geq 10)\), joka
todennäköisyyslaskennan komplementtisäännön mukaan voidaan kirjoittaa muotoon
\(P(X<30|X\geq 10)=1-P(X\geq 30| X\geq 10)\). Edelleen eksponenttijakauman
unohdusominaisuuden mukaan saadaan nyt \(P(X\geq 30 |X\geq 10)=P(X\geq 20)\).
Kun tämä yhdistetään aiempiin, niin saadaan
\(P(X<30|X\geq 10)=1-(1-P(X<20))=P(X<20)\). Todennäköisyyden lukuarvo
saadaan edelleen eksponenttijakauman kertymäfunktiosta:
\(P(X<20)=F(20)= 1-e^{ \left( -\frac{20}{30} \right) }=0.487\).
4.2 Poisson-jakauma
Diskreetin satunnaismuuttujan \(X\) sanotaan olevan Poisson-jakautunut parametrilla \(\lambda \>0\), jos sen pistetodennäköisyysfunktio (ptnf) on \[f(x;\lambda)=P(X=x)=\begin{cases} \frac{\lambda^x e^{-\lambda}}{x!}&,& \text{ kun } x=0,1,2,... \\ 0& & \text{muulloin} \end{cases}.\]
Merkintä Poisson-jakautuneelle satunnaismuuttujalle \(X\) on \(X\sim Poisson(\lambda)\). Poisson-jakaumaa käytetään usein kuvaamaan riippumattomien harvinaisten tapahtumien lukumäärää sopivassa mittayksikössä ja jossa sattumisten keskimääräinen lukumäärä mittayksikössä on \(\lambda.\) Tarkasteltava mittayksikkö on tyypillisesti aika, mutta se voi olla myös esimerkiksi pituus- tai tilavuusyksikkö tai muu suure.
4.2.1 Poisson-jakauman ominaisuuksia
Satunnaismuuttujalle \(X\sim Poisson(\lambda)\) on voimassa
- Odotusarvo: \(E(X)=\lambda\)
- Varianssi:\(Var(X)=\lambda\)
- Poisson-jakauman kertymäfunktio saadaan summaamalla yksittäiset pistetodennäköisyydet: \[F(x;\lambda)= \sum_{z=0}^x\frac{\lambda^z e^{-\lambda}}{z!}\]
- Riippumattomien satunnaismuuttujien \(X_i \sim Poisson(\lambda_i)\) summalle \(Y=\sum_{i=1}^n X_i\) on voimassa \(Y \sim Poisson\left(\sum_{i=1}^n \lambda_i\right)\) eli summan Poisson-jakauman parametri on yksittäisten parametrien summa. Tässä parametrit \(\lambda_i\) voivat siis olla toisistaan poikkeavia.
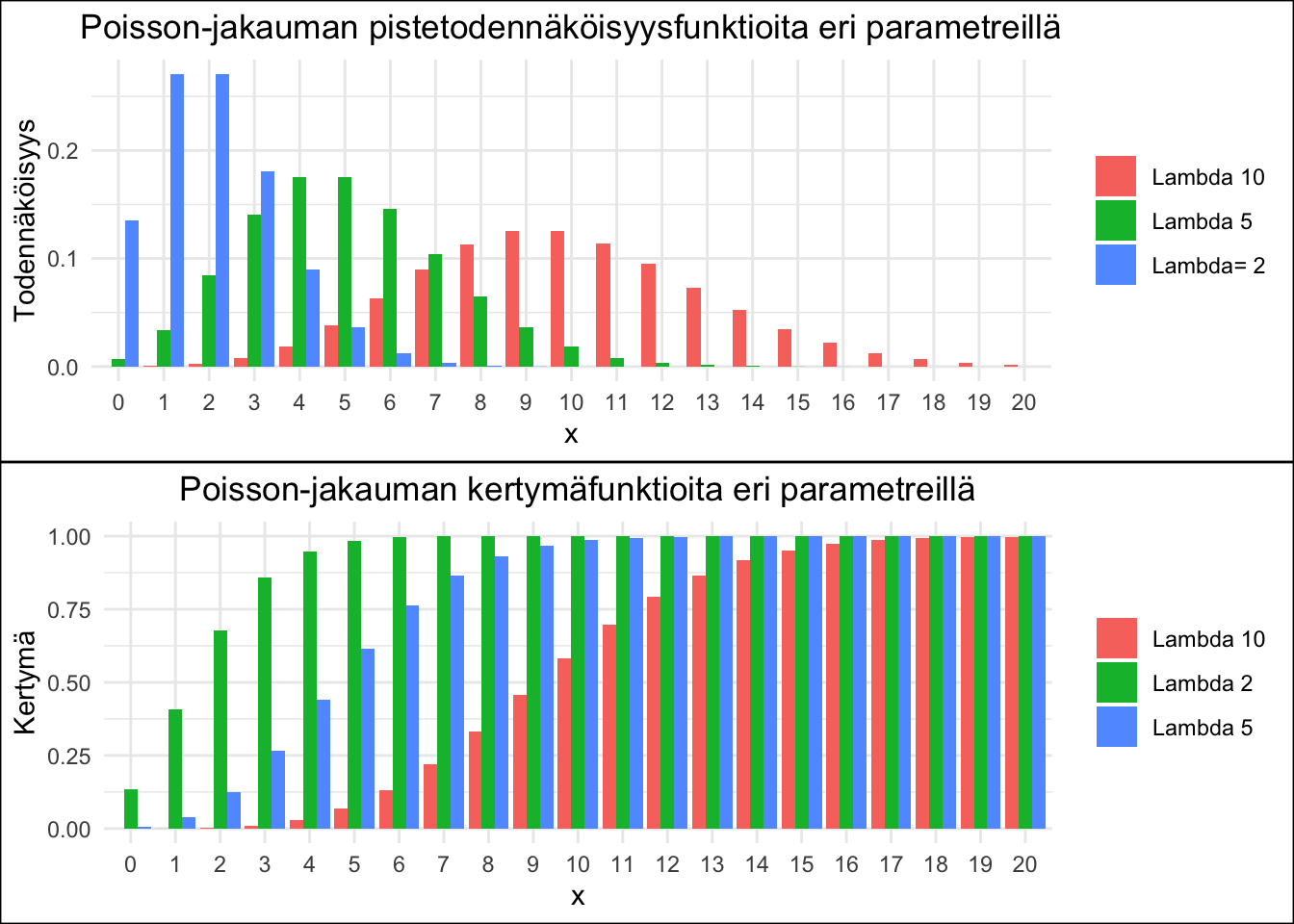
Figure 4.2: Poisson-jakauman ptnf ja kertymäfunktiot kolmella eri parametrillä.
4.2.2 Todennäköisyyksien lasku Poisson-jakaumasta
Todennäköisyyksien laskuun voidaan käyttää suoraan pistetodennäköisyysfunktiota ja tarvittaessa soveltaen erilaisia summakaavoja sekä normaaleja todennäköisyyslaskennan peruslaskusääntöjä. R:llä relevantit valmisfunktiot ovat
dpois(x, lambda): kertoo pistetodennäköisyyden arvon lukumäärälle \(x\)ppois(x,lambda): kertoo kertymäfunktion arvon kohdassa \(x\)qpois(p,lambda): kertoo kertymäfunktion käänteisfunktion arvon todennäköisyydelle \(p\)
Esimerkki 4.2.2.1
Oletetaan, että \(X\sim Poisson(3)\). Laske \(P(X<2)\).
Ratkaisu
Todetaan, että haluttu todennäköisyys koostuu alkeistapauksista
\(P(X=0)\) ja \(P(X=1)\). Kysytty todennäköisyys on siis \(P(X<2)=
\sum_{x=0}^{1} \frac{3^x}{x!}e^{-3} =
\frac{3^0}{0!}e^{-3}+\frac{3^1}{1!}e^{-3}\) \(=e^{-3}+3e^{-3} =
4e^{-3} = 0.199.\)
Sama ratkaisu saadaan R:llä myös suoraan käyttäen ppois(1,lambda=3) tai vastaavasti dpois(0,lambda=3)+dpois(1,lambda=3).
Esimerkki 4.2.2.2
Oletetaan, että \(X\sim Poisson(7)\). Laske \(P(X\geq2)\).
Ratkaisu
Todennäköisyys \(P(X\geq2)\) saadaan helposti
komplementtitodennäköisyytenä \(1-P(X<2)\). Käytetään parametriä
\(\lambda=7\) ja lasketaan vastaavalla tavalla kuin edellisessä
esimerkissä, jolloin saadaan \(P(X\geq 2)=1-\left(\sum_{x=0}^{1}
\frac{7^x}{x!}e^{-7}\right)=1-(e^{-7}+7e^{-7})\)
\(=1-7e^{-7}=0.9927049\). R:llä lukuarvo saadaan komennolla 1-ppois(1,lambda=7).
Esimerkki 4.2.2.3
Oletetaan, että Helsingissä tapahtuu keskimäärin 20 peltikolaria päivässä, joista noin 25 % johtaa auton lunastukseen. Millä todennäköisyydellä päivän
aikana tapahtuu 1-5 lunastukseen johtavaa peltikolaria, kun
peltikolarien oletetaan jakautuneen Poisson-jakauman mukaisesti?
Ratkaisu
Merkitään, että X=lunastukseen joutuneiden autojen
lkm. Nyt siis tehtävänannon mukaan \(X \sim Poisson (\lambda)\), jossa
\(\lambda=20\cdot0.25=5\). Kysytty todennäköisyys \(P(1\leq X \leq 5)\)
koostuu tapauksista \(P(X=1)\), ..., \(P(X=5)\). Lukuarvoksi saadaan
siis \(P(1\leq X \leq 5)=\left( \frac{5}{1!} + \frac{5^2}{2!} +
\frac{5^3}{3!}+\frac{5^4}{4!}+\frac{5^5}{5!}
\right)e^{-5}=0.6092227.\) R:llä saadaan sama tulos komennolla ppois(5,lambda=5)-ppois(0,lambda=5).
Esimerkki 4.2.2.4
Oletetaan, että \(X\sim Poisson(5.5)\). Laske raja \(x_0\), jolla \(P(X\leq x_0)=0.95\).
Ratkaisu
Tarkastellaan vastaavanlaista summaa
kuin aiemmassa tehtävässä \(\sum_{x}\frac{{5.5}^x
e^{-5.5}}{x!}=\left( \frac{5.5}{1!} + \frac{{5.5}^2}{2!} +
\frac{{5.5}^3}{3!}+... \right)e^{-5.5}\). Tästä tarkastelusta
saadaan \(P(X\leq 9)=0.94622253\) ja \(P(X\leq 10)=0.974748749\).
Tehtävän substanssista riippuen valitaan jompi kumpi näistä ratkaisuista
\(x_0=9\) tai \(x_0=10\).
4.2.3 Poisson-jakauma vs. binomijakauma
Tyypillisin Poisson-jakauman sovellus on mallintaa erilaisia harvinaisten tapahtumien lukumääriä. Tähän voitaisiin käyttää myös aiemmista opinnoista tuttua binomijakaumaa. Näillä kahdella jakaumalla on kuitenkin kaksi merkittävää käytännöllistä eroa:
Poisson-jakauma parametrisoidaan odotusarvollaan eli keskimääräisellä odotettavissa olevalla onnistumisten lukumäärällä sopivassa mittayksikössä eli eräänlaisella bulkkisuureella. Vastaavasti binomijakauma perustuu monen yksittäisen riippumattoman toiston summan tarkasteluun, jossa jokaisen yksittäisen tapahtuman onnistumistodennäköisyys \(p\) tunnetaan. Binomijakaumassa oletaan siis, että jokainen jokainen yksittäinen (Bernoulli-jakautunut) satunnaismuuttuja tunnetaan tarkkaan. Poisson-jakaumassa vaatimus on lievempi - ilmiö tunnetaan vain suurella ryhmätasolla. Poisson-jakaumaan liittyvän keskimääräisen tapahtumavauhdin \(\lambda\) konsepti voi myös olla käsitteellisesti huomattavasti helpompi ja mielekkäämpi suure kuin yksittäisen toistokokeen onnistumistodennäköisyys \(p\) binomijakaumassa. Tämän parametrin lukuarvo tai arvoalue voi myös olla huomattavasti helpompi selvittää tilastollisista aineistoista, esimerkiksi seurantadatasta.
Binomijakaumasta \(Bin(N,p)\) on mahdollista saada enintään \(N\) tapahtumaa tai onnistumista, kun vastaavasti Poisson-jakaumalla satunnaismuuttujan arvoille ei ole mitään ehdotonta ylärajaa onnistumisille. Huomaa myös, että vaikka Poisson-jakauman parametriä voidaankin estimoida käytännön aineistosta laskemalla keskimääräinen päätetapahtumien lukumäärä tietystä joukosta, niin tämä ei kuitenkaan aseta Poisson-jakautuneelle satunnaismuuttujalle mitään ylärajaa.
Lopputulemana edellisistä voidaankin siis sanoa, että binomijakauma on käytännön sovellusten kannalta rajoittavampi todennäköisyysjakauma kuvaamaan käytännön ilmiöitä, sillä binomijakaumaan vaaditaan enemmän tietoa ja reunaehtoja.
4.2.4 Binomi-jakauman Poisson-approksimaatio
Teorian mukaan Poisson-jakaumaa voidaan käytenkin käyttää binomijakauman asemasta kuvaamaan harvinaisia tapahtumatodennäköisyyksiä pitkissä toistosarjoissa, mikäli binomijakauman \(N\) on riittävän suuri ja \(p\) on riittävän pieni. Tällöin Poisson-jakauman parametrina käytetään binomijakauman odotusarvoa \(\lambda=Np\). Tämä binomijakauman approksimaatio Poisson-jakaumalla on yleensä riittävän hyvä, jos binomijakauman parametrit \(N>20\) ja \(p<0.05\). Parametreillä \(N>100\) ja \(p<0.1\) approksimaatiota sanotaan hyväksi. Nämä approksimaation hyvyyttä kuvaavat ilmaisut ovat kuitenkin vain yhden konvention mukaisia ilmaisuja.
Huomautus. Binomijakauman Poisson-approksimaatio on luonteeltaan analoginen kuin Binomijakauman normaaliapproksimaatio (ks. tilastotieteen perusteet). Yhdistämällä nämä huomiot voidaan edelleen päätellä, että Poisson-jakaumaa on tietyin oletuksin mahdollista approksimoida normaalijakaumalla.
Esimerkki 4.2.4.1
Sormileluja valmistava Lohjalainen yritys on havainnut, että heidän
tuotteistaan 0.35 prosenttia on virheellisiä. Laske Poisson-approksimaatio ja tarkka binomitodennäköisyys, että seuraavasta tuhannen
kappaleen tuotantoerästä heille palautetaan vain yksi lelu?
Ratkaisu
Oletetaan, että kyseessä rikkinäisten lelujen jakauma
tuotantoerässä noudattaa Binomijakaumaa parametreillä \(p=0.0035\) ja
\(N=1000\). Nyt Poisson-approksimaation mukaan
\(\lambda=Np=1000\cdot0.0035=3.5\) ja approksimaatio on \(P(X =
1)=\frac{\lambda^x}{x!}e^{-\lambda} =
\frac{{3.5}^1}{1!}e^{-3.5}\) = \(3.5\cdot e^{-3.5}=0.1057\).
Vastaavasti binomijakauman laskutavalla saadaan: \(P(X=1)= \binom{n}{x}
p^x \cdot(1-p)^{n-x}\) \(= \binom{1000}{1}\cdot0.0035\cdot0.9965^{999}=
0.1054\). R:llä lukuarvot saadaan komennoilla
dpois(1,lambda=3.5) ja dbinom(1,size=1000,prob=0.0035).
4.3 Poisson(-prosessin) ja eksponenttijakauman yhteys
Johdanto:
Määritellään diskreetti satunnaismuuttuja \(X\) niiden tapahtumien lukumääräna, jotka sattuvat aikavälillä \([0,t]\)*. Tällöin sopivin
oletuksin satunnaismuuttuja \(X\) noudattaa Poisson-jakaumaa parametrillä \(\nu
t\) eli \(X \sim Poisson(\nu t)\). Suure \(\nu t\) kuvaa tässä
tapahtumien keskimääräistä lukumäärää aikavälillä, jonka pituus on
\(t\) aikayksikköä.
Kun \(X \sim Poisson (\nu t)\) ja jatkuva satunnaismuuttuja \(Z\) = tapahtumien väliaika tai aika ensimmäisen tapahtuman sattumiseen, niin tällöin \(Z \sim Exp(\nu t)\) eli lyhyesti sanottuna: Poisson-prosessin tapahtumien väliajat ovat eksponentiaalisesti jakautuneita.
Esimerkki 4.3.1
Eräällä 2000 työntekijän tehtaalla korvattavien työtapaturmien
määrä viikossa noudattaa Poisson-jakaumaa parametrilla \(\lambda = 0.4\). Millä
todennäköisyydellä kahden työtapaturman välinen aika on alle kaksi viikkoa?
Ratkaisu
Poisson-jakauman mukainen tapaturmien keskimääräinen määrä
viikossa on 0.4 tapahtumaa viikossa, joten tapahtumien väliaikojen
keskimääräinen väliaika on 1/0.4 viikkoa, joka on eksponenttijakauman
odotusarvo=\(1/\lambda\). Väliajat saadaan siis eksponenttijakaumasta,
jonka parametri \(\lambda=0.4\) Nyt voidaan siis helposti laskea \(P(T
\leq 2)=1-e^{-0.4\cdot 2}=0.550671\). R:llä lukuarvo saadaan komennolla
pexp(2,rate=0.4).
4.4 Gamma-jakauma
Jatkuvan satunnaismuuttujan \(X\) sanotaan olevan Gamma-jakautunut parametreilla \(k>0\) ja \(\theta>0\), jos sen tiheysfunktio (tf) on \[ f(x;k,\theta) = \begin{cases} \frac{1}{\Gamma (k)\theta^k} x^{k-1}e^{-\frac{x}{\theta}}&,& \text{kun } x\geq 0 \\ 0&,& \text{muulloin} \end{cases}.\] Merkintä tällä tavalla gamma-jakautuneelle satunnaismuuttujalle on \(X\sim Gamma(k,\theta)\). Yllä olevassa tiheysfunktiomuodossa parametriä \(k\) sanotaan Gamma-jakauman muotoparametriksi (shape) ja parametriä \(\theta\) skaalaparametriksi (scale). Gamma-jakaumalle käytetään melko yleisesti myös toisenlaista parametrisointia, jossa tiheysfunktio kirjoitetaan muotoon \[f(x;\alpha,\beta)=\frac{\beta^{\alpha}}{\Gamma (\alpha)} x^{\alpha-1}e^{-\beta x} , \text{ kun } x \geq 0.\] Tässä parametrisoinnissa \(\alpha\):aa kutsutaan edelleen muotoparametriksi, mutta parametria \(\beta\) kutsutaan rate-parametriksi. Jälkimmäisen Gamma-jakauman parametrisoinnin yhteys aiempaan parametrisointiin on \(rate=1/scale\). Tässä materiaalissa käytetään ensin mainittua parametrisointia, ellei muuta ilmoiteta.
Gamma-jakaumaa käytetään moninaisesti mallintamaan erilaisia positiivisia satunnaismuuttujia, kuten odotusaikoja ja muita intensiteettiprosesseja. Gamma-jakaumaa käytetään usein myös kvantifioimaan epävarmuutta tai uskottavuutta esimerkiksi hierarkisissa Bayes-malleissa.
4.4.1 Gamma-jakauman ominaisuuksia
Satunnaismuuttujalle \(X\sim Gamma(k,\theta)\) on voimassa
- Odotusarvo: \(E(X)=k\theta\)
- Varianssi: \(Var(X)=k\theta ^2\)
Lisäksi
- \(Gamma(1,\theta)=Exp(1/\theta)\)
- Riippumattomien samoinjakautuneiden satunnaismuuttujien \(X_i \sim Exp(\lambda)\) summalle \(Y=\sum_{i=1}^n X_i\) pätee \(Y \sim Gamma(n,\lambda)\)
- Riippumattomien satunnaismuuttujien \(X_i \sim Gamma(k_i,\lambda)\) summalle summalle \(Y=\sum_{i=1}^n X_i\) pätee \(Y \sim Gamma \left(\sum_{i=1}^n k_i,\lambda\right)\)
Huomautus Seurauksena yllä olevasta kohdasta 2 sekä eksponenttijakauman ja Poisson-prosessin yhteydestä saadaan tulos: jos tapahtumalukumäärä \(X\sim Poisson(\lambda)\), jolloin siis odotusaika ensimmäiseen tapahtumaan (tai tapahtumien välillä) on jakaantunut kuten \(Exp(\lambda)\), niin odotusaika \(k\):n tapahtuman sattumiselle on jakaantunut kuten \(Gamma(k,1/\lambda)\).
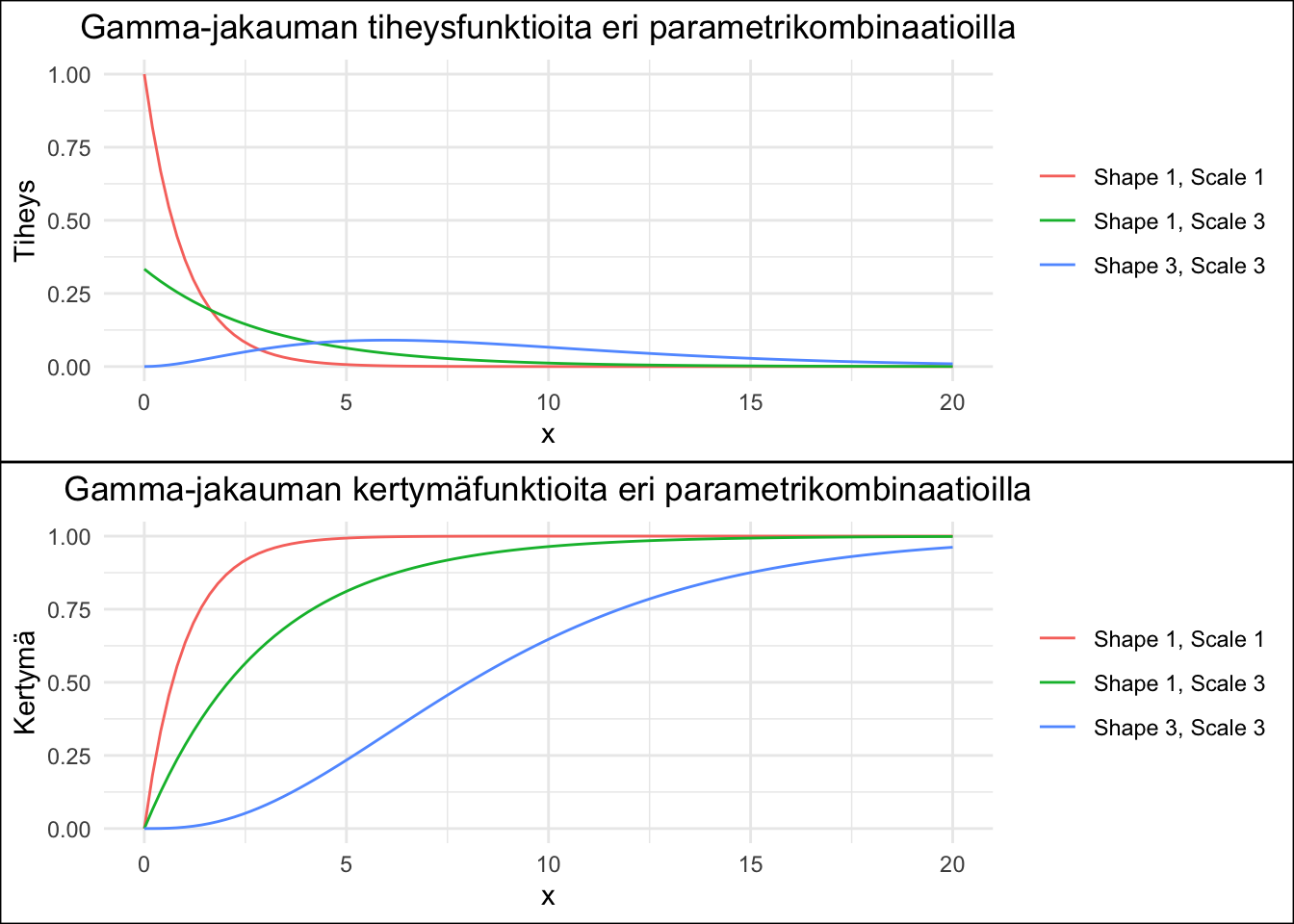
Figure 4.3: Gammajakauman tiheys- ja kertymäfunktioita kolmella eri parametrikombinaatiolla.
4.4.2 Todennäköisyyksien lasku Gamma-jakaumasta
Gamma-jakauman kertymäfunktiota ei voida ilmoittaa suljetussa muodossa, ja todennäköisyyksien laskentaan tarvitaan useimmiten ohjelmistoja. Tilastollisten ohjelmistojen ja mahdollisten taulukoiden kohdalla on kuitenkin oltava tarkkana mihin Gamma-jakauman parametrisointiin lukuarvot perustuvat. R:llä relevantit valmisfunktiot ovat
dgamma(x, shape, scale): kertoo tiheysfunktion arvon kohdassa \(x\)pgamma(x, shape, scale): kertoo kertymäfunktion arvon kohdassa \(x\)qgamma(p, shape, scale): kertoo kertymäfunktion käänteisfunktion arvon todennäköisyydelle \(p\)
Esimerkki 4.4.2.1
Oletetaan,
että \(X\sim Gamma(4,1)\). Laske \(P(X<3)\).
Ratkaisu
Lasketaan kertymäfunktio välillä \([0,3)\). Tätä ei voida ilmoittaa
suljetussa muodossa, mutta tähän voidaan käyttää ohjelmistoja. R:llä tämä onnistuu komennolla pgamma(3,shape=4,scale=1) josta saadaan lukuarvoksi
\(P(X<3)=0.353\).
Esimerkki 4.4.2.2
Oletetaan, että \(X\sim Gamma(6,2)\). Laske \(P(2<X<4)\).
Ratkaisu
Lasketaan kertymäfunktio välillä \((2,4)\), joka saadaan
erotuksena \(F(4;6,2)-F(2;6,2)\), jossa funktio \(F\) on Gamma-jakauman
kertymäfunktio. Lukuarvo saadaan R-komennolla
pgamma(4,shape=6, scale=2)-pgamma(2, shape=6, scale =2), josta
saadaan \(P(2<X<4)=0.016\).
Esimerkki 4.4.2.3
Oletetaan, että puhelinoperaattorin neuvontalinjat käsittelevät asiakkaan ongelman keskimäärin 20 minuutissa, ja oletetaan työaikojen jakautuvan
eksponentiaalisesti. Laske millä todennäköisyydellä yksi neuvontalinja
pystyy käsittelemään kahdeksan asiakkaan ongelmat alle kahdessa
tunnissa.
Ratkaisu
Keskimääräinen työaika asiakasta kohti on nyt \(1/3\) tuntia, ja
koska eksponenttijakauman odotusarvo on \(1/\lambda\), niin väliajat
noudattavat siis jakaumaa \(Exp(3)\). Käytetään Gamma-jakauman lisäominaisuutta
hyväksi, jonka mukaan kahdeksan tapahtuman yhteenlaskettu odotusaika \(X\)
noudattaa jakaumaa \(Gamma(8,1/3)\). Lasketaan nyt todennäköisyys \(P(X< 2)\). R-komennolla pgamma(2,shape=8,scale=1/3) saadaan lukuarvoksi \(P(X<2)=0.256\).
Esimerkki 4.4.2.4
Yrityksen tuotantolinja tuottaa keskimäärin 4.7 tuotetta aikayksikössä. Mikä on 95
prosentin prosenttipiste ajalle saada 200 tuotetta valmiiksi kun
valmistumisaikojen odotetaan noudattavan eksponentiaalista jakaumaa?
Ratkaisu
Kun keskimääräinen lukumäärä on 4.7 tuotetta
aikayksikössä, niin keskimääräinen väliaika on selvästi 1/4.7, ja
noudattaa siis jakaumaa \(Exp(4.7)\). Gamma-jakauman lisäominaisuuden
perusteella aika 200 tuotteen valmistumiseen noudattaa jakaumaa
\(Gamma(200,1/4.7)\). Nyt haetaan siis pistettä \(x_0\), jolla
\(P(X\leq x_0)=0.95\). Tämä saadaan R-komennolla qgamma(0.95, shape=200, scale=1/4.7), josta saadaan lukuarvoksi \(x_0=47.620\).
Esimerkki 4.4.2.5
Laske esimerkin 4.1.4.3 ratkaisu käyttäen Gamma-jakauman ominaisuuksia.
Ratkaisu
Gamma-jakauman tietojen mukaan
\(Exp(\lambda)=Gamma(1,1/\lambda)\). Nyt siis \(T\sim Gamma(1,45.13)\). R-komennolla qgamma(0.95, shape=1, scale=45.13) saadaan lukuarvoksi \(t_0=135.197\).
Esimerkki 4.4.2.6
Tiedetään, että Gamma-jakauman vaihtoehtoisen parametrisoinnin mukaan on voimassa:
\(\frac{\alpha}{\beta ^2}=0.32\) ja vauhtiparametri (*rate*) on 5
tapahtumaa kolmessa aikayksikössä. Laske todennäköisyys, että
\(P(X >1)\).
Ratkaisu
Kun tiedetään, että vaihtoehtoisessa
parametrisoinnissa \(\frac{\alpha}{\beta ^2}=0.32\) ja
\(\beta=5/3\) (per yksi aikayksikkö). Tästä saadaan
\(\alpha=0.32\cdot(5/3)^2\). Kysytty todennäköisyys \(P(X\>1)\) saadaan
komplementtitodennäköisyyden avulla \(P(X\>1)=1-P(X\leq 1)\).
Lukuarvoo saadaan R-komennolla 1-pgamma(1, shape=0.32*(5/3)^2, scale=1/(5/3)). Huomaa, että R:llä voidaan laskea lukuarvo myös suoraan käyttäen scale-parametrin sijasta rate-parametriä: 1-pgamma(1, shape=0.32*(5/3)^2, rate=5/3). Kummallakin tavalla saadaan tulokseksi
saadaan tulokseksi \(P(X>1)=0.248\).
4.5 \(\chi^2\) -jakauma
Oletetaan, että riippumattomat satunnaismuuttujat \(X_1,X_2,\ldots,X_n\) noudattavat standardinormaalijakaumaa \(N(0,1)\) eli \(X_i \sim N(0,1),i=1,\ldots,n\). Tällöin satunnaismuuttuja \[X=\sum_{i=1}^n X_i^2\] noudattaa \(\chi ^2\) (*khi toiseen*) -jakaumaa parametrillä \(n\) ja sen tiheysfunktio on muotoa \[f(x;n)=\frac{1}{2^{\frac{n }{2}}\Gamma\left(\frac{n}{2}\right)}x^{\frac{n}{2}-1} e^{-\frac{x}{2}}, \text{ kun } x\geq 0\] ja muutoin nolla. Tässä tiheysfunktiossa merkintä \(\Gamma(\cdot)\) tarkoittaa ns. gamma-funktiota. Huomaa, että Gamma-funktiota ei tule sekoittaa gamma-jakaumaan tai sen tiheysfunktioon.
Merkintä tälle jakautumiselle on \(X \sim \chi ^2(n)\). Tämän jakauman parametriä \(n\) kutsutaan vapausasteeksi ja se kuvastaa tämän kurssin puitteissa yhteenlaskettavien neliöityjen satunnaismuuttujien lukumäärää (yleisemmin tämän vapausasteparametrin ei tarvitse olla kokonaisluku). Huomaa, että \(\chi ^2\)-jakauman tiheysfunktiolle on kirjallisuudessa myös vaihtoehtoisia esitysmuotoja.
Tähän jakaumaan päädytään myös muista konteksteista, mutta edellä kuvattu kehikko riippumattomien neliöityjen satunnaismuuttujien summana toimii teoreettisena pohjana moneen tilastolliseen testiin, joihin tutustutaan myöhemmin tässä dokumentissa.
4.5.1 \(\chi ^2\) -jakauman ominaisuuksia:
- Odotusarvo: \(E(X)=n\)
- Varianssi: \(Var(X)=2n\)
- Tiheysfunktio on epäsymmetrinen ja oikealle vino (vähenevät \(n\):n kasvaessa)
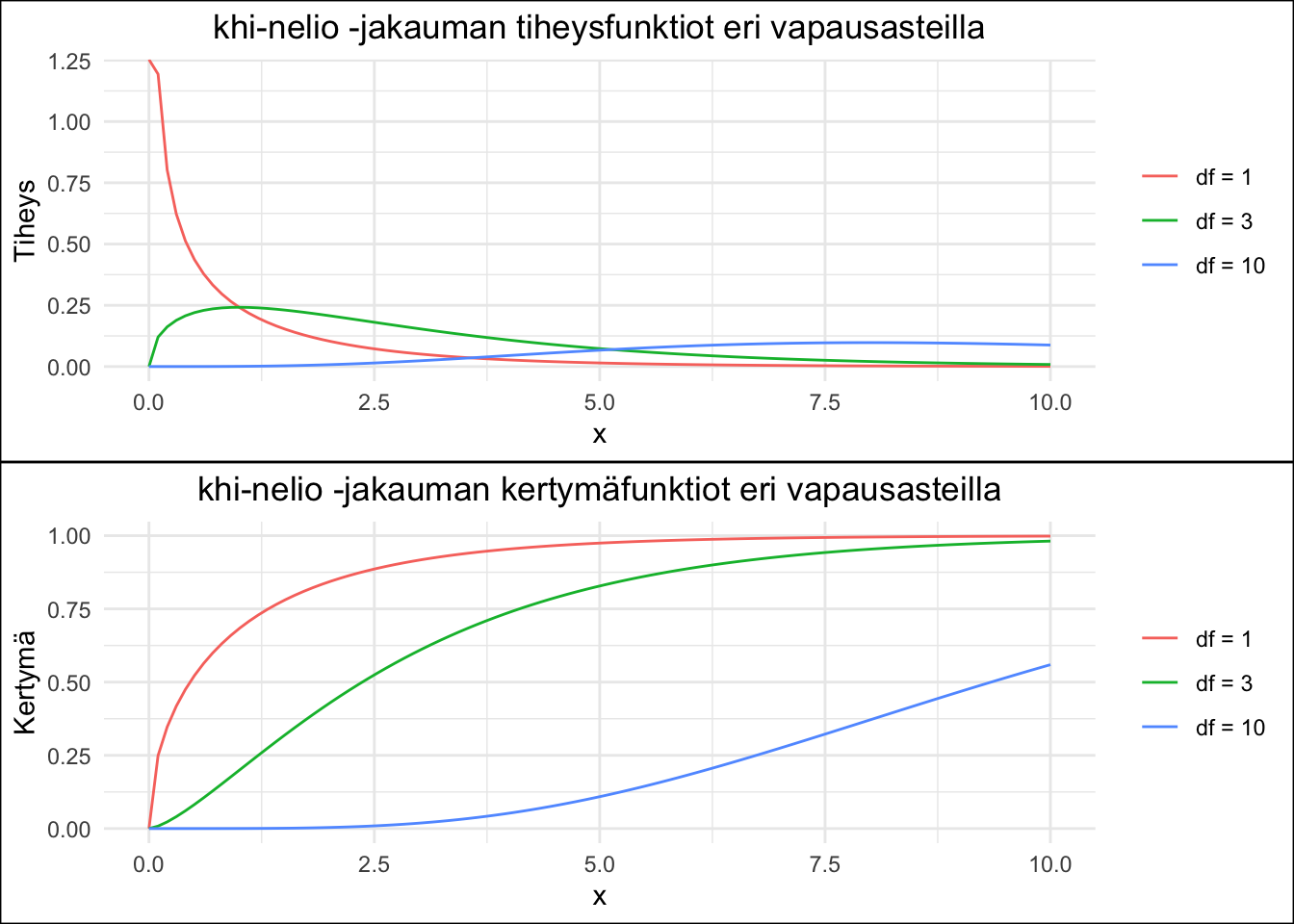
Figure 4.4: Chi-toiseen jakauman tiheys- ja kertymäfunktiot kolmella eri parametrillä.
4.5.2 Todennäköisyyksien laskeminen \(\chi ^2\)-jakaumasta
\(\chi^2\)-jakauman kertymäfunktiota ei voida esittää yksinkertaisesti ns. suljetussa muodossa ja kertymäfunktion arvot joudutaan määrittämään käyttäen tietokoneohjelmia tai tilastollisia taulukoita. R:llä relevantit valmisfunktiot ovat
dchisq(x,deg_freedom): kertoo tiheysfunktion arvon kohdassa \(x\)pchisq(x,deg_freedom): kertoo kertymäfunktion arvon kohdassa \(x\)qchisq(p,deg_freedom): kertoo kertymäfunktion käänteisfunktion arvon todennäköisyydelle \(p\)
4.6 F-jakauma
Oletetaan, että riippumattomat
satunnaismuuttujat \(X_1,X_2,\ldots,X_n\) ja \(Y_1,Y_2,\ldots,Y_m\)
noudattavat standardinormaalijakaumaa \(N(0,1)\) eli \(X_i,Y_j \sim
N(0,1)\), ja kun määritellään satunnaismuuttujat \(X=\sum_{i=1}^n
X_i^2\) ja \(Y=\sum_{i=1}^m Y_i^2\). Tällöin keskimääräisten neliösummien
osamääränä määritelty satunnaismuuttuja
\[F=\frac{\frac{1}{m}Y}{\frac{1}{n}X}=\frac{nY}{mX}\] noudattaa
(keskeistä)F-jakaumaa
parametreillä \(m\) ja \(n\) ja sen tiheysfunktio on muotoa
\[f(x;m,n)=\frac{ \Gamma
\left( \frac{m+n}{2} \right) } { \Gamma \left( \frac{n}{2}
\right) \Gamma \left( \frac{m}{2} \right) } \left( \frac{m}{n}
\right) ^{\frac{m}{2}} \frac{ x^{\frac{m-2}{2} }} {
\left(1+\frac{mx}{n} \right)^{-\frac{m+n}{2}} } , \text{ kun }
x\geq 0\] ja muutoin nolla. Merkintä tälle jakautumiselle on \(F \sim
F(m,n)\). Tämän jakauman parametrejä \(m\) ja \(n\) kutsutaan
vapausasteiksi ne kuvastavat yhteenlaskettavien neliöityjen
satunnaismuuttujien lukumäärää osamääräsuureessa \(F\).
Huomaa, että \(F\)-jakauman tiheysfunktiolle myös toisia vaihtoehtoisia
esitysmuotoja, jotka voivat näyttäytyä hyvinkin erilaisilta.
Tähän jakaumaan
päädytään myös muista konteksteista ja F-jakauma voidaan nähdä
esimerkiksi erikoistapauksena myös eräistä muista jakaumista.
F-jakaumalla on käytännön merkitys erityisesti tilastollisessa testauksessa,
jossa se toimii referenssijakaumana esimerkiksi
F-testeissä sekä
varianssianalyysissä(ANOVA).
4.6.1 F-jakauman ominaisuuksia:
Satunnaismuuttujalle \(F\sim F(m,n)\) on voimassa
- Odotusarvo: \(E(F)=\frac{n}{n-2}\), \(n>2\)
- Varianssi: \(Var(F)=\frac{2n^2(m+n-2)}{m(n-2)^2(n-4)}\), \(n>4\)
- Jos \(\beta=P( F_{m,n}>x)\), niin tällöin komplementtitodennäköisyydelle on voimassa \(1-\beta=P(F_{m,n}\leq x)=P\left(F_{n,m}\leq \frac{1}{x}\right)\)
- Tiheysfunktio on epäsymmetrinen ja oikealle vino
- Jos alkuperäisen satunnaismuuttujan \(F=\frac{\frac{1}{m}Y}{\frac{1}{n}X}=\frac{nY}{mX}\) sijaan tarkastellaankin satunnaismuuttujaa \(1/F=\frac{\frac{1}{n}X}{\frac{1}{m}Y}=\frac{mX}{nY}\), niin tälle on voimassa \(\frac{1}{F} \sim F(n,m)\) (huomaa vapausasteiden järjestys). Tämä tulos on myöhemmin merkityksellinen varianssitestauksessa, jossa tarkastellaan kahden otoksen varianssien suhteita.
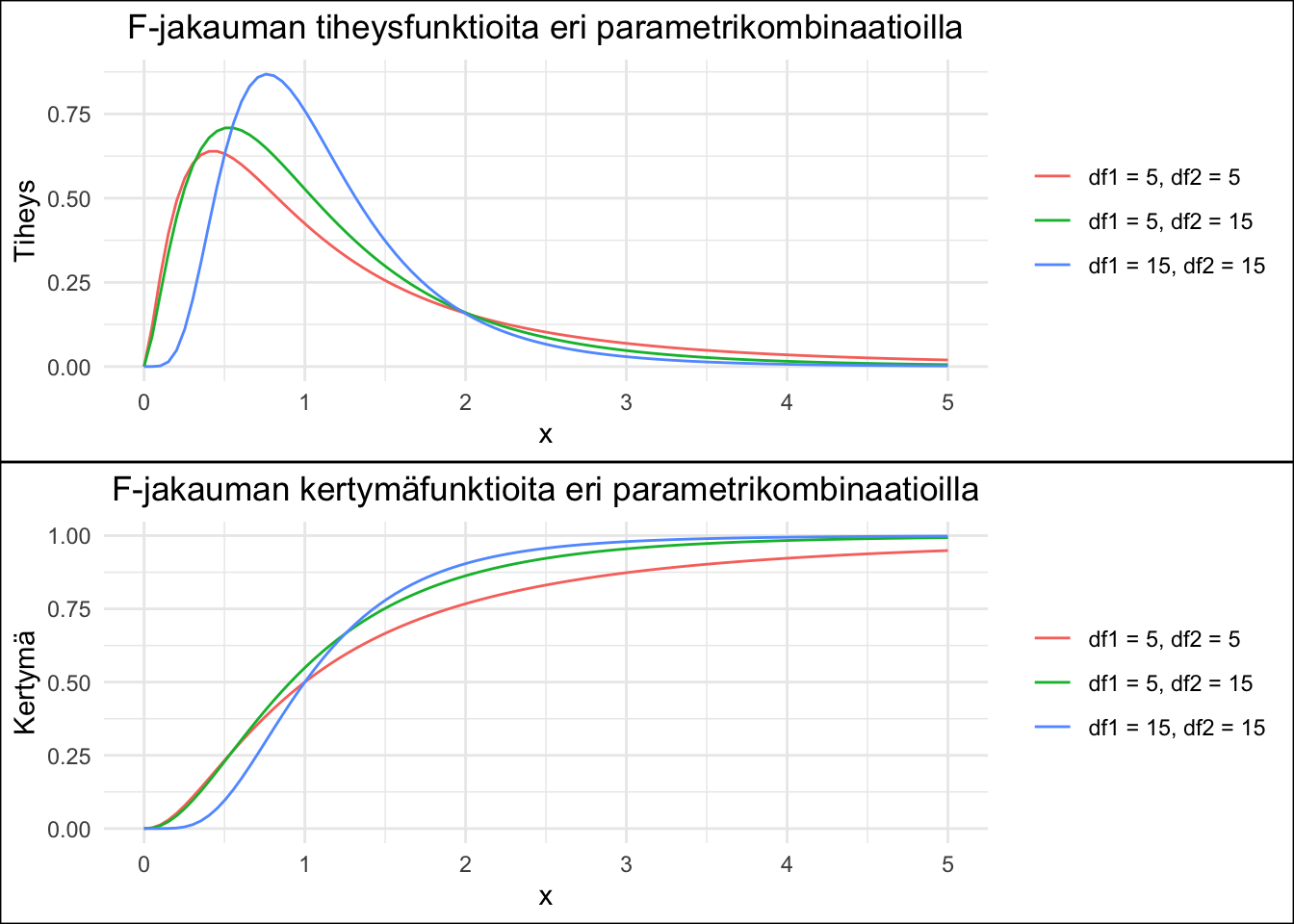
Figure 4.5: F-jakauman tiheys- ja kertymäfunktioita kolmella eri parametrikombinaatiolla.
4.6.2 Todennäköisyyksien laskeminen F-jakaumasta
F-jakauman tiheysfunktion hankalan muodon takia kertymäfunktion ja kvantiilien laskut tehdään yksinomaan käyttäen tietokoneita tai taulukoita. R:llä relevantit valmisfunktiot ovat
df(x,df1,df2): kertoo tiheysfunktion arvon kohdassa \(x\)pf(x,df1,df2): kertoo kertymäfunktion arvon kohdassa \(x\)qf(p,df1,df2): kertoo kertymäfunktion käänteisfunktion arvon todennäköisyydelle \(p\)
4.7 (Studentin) t-jakauma
Oletetaan, että riippumattomat satunnaismuuttujat \(X_1,X_2,\ldots,X_n\) ja näistä riippumaton \(Y\) noudattavat kaikki standardinormaalijakaumaa \(N(0,1)\) ja määritellään lisäksi satunnaismuuttuja \(X=\sum_{i=1}^n X_i^2\) (jolle \(\chi^2\) jakauman teorian perusteella \(X \sim \chi^2(n)\)). Tällöin riippumattomista satunnaismuuttujista \(X\) ja \(Y\) johdettu muuttuja \[T=\frac{Y}{\sqrt{\frac{X}{n}}}\] noudattaa (Studentin)t-jakaumaa parametrillä \(n\) ja sen tiheysfunktio on muotoa \[t(x;n)=\frac{ \Gamma \left( \frac{n+1}{2} \right) } { \sqrt{n\pi} \Gamma \left( \frac{n}{2} \right) } \left( 1+ \frac{x^2}{n} \right) ^{-\frac{n+1}{2}}.\] Merkintä tälle jakautumiselle on \(T \sim t(n)\). Tämän jakauman parametriä \(n\) kutsutaan vapausasteeksi ja se kuvastaa yhteenlaskettavien neliöityjen satunnaismuuttujien lukumäärää nimittäjässä osamääräsuureen \(T\) määrittelyssä. Myös t-jakauman tiheysfunktiosta esiintyy kirjallisuudessa hieman erilaisia vaihtoehtoisia esitysmuotoja.
T-jakaumalla jakaumalla on suuri merkitys erityisesti tilastollisessa testauksessa, jossa jakauma toimii referenssijakaumana t-testien perheessä, joka on yksi merkittävimmistä testiperheistä tilastollisessa testauksessa.
4.7.1 t-jakauman ominaisuuksia
Satunnaismuuttujalle \(T \sim t(n)\) on voimassa
- Odotusarvo: \(E(T)=0\),
- Varianssi: \(Var(T)=\frac{n}{n-2}\), kun \(n>2\)
- Jakauma on symmetrinen odotusarvonsa suhteen.
- Pienillä vapausasteparametreillä tiheysfunktion kuvaaja muistuttaa standardinormaalijakaumaa, mutta on paksuhäntäisempi. T-jakauman vapausasteparametrin kasvaessa kuvaaja lähestyy normaalijakaumaa.
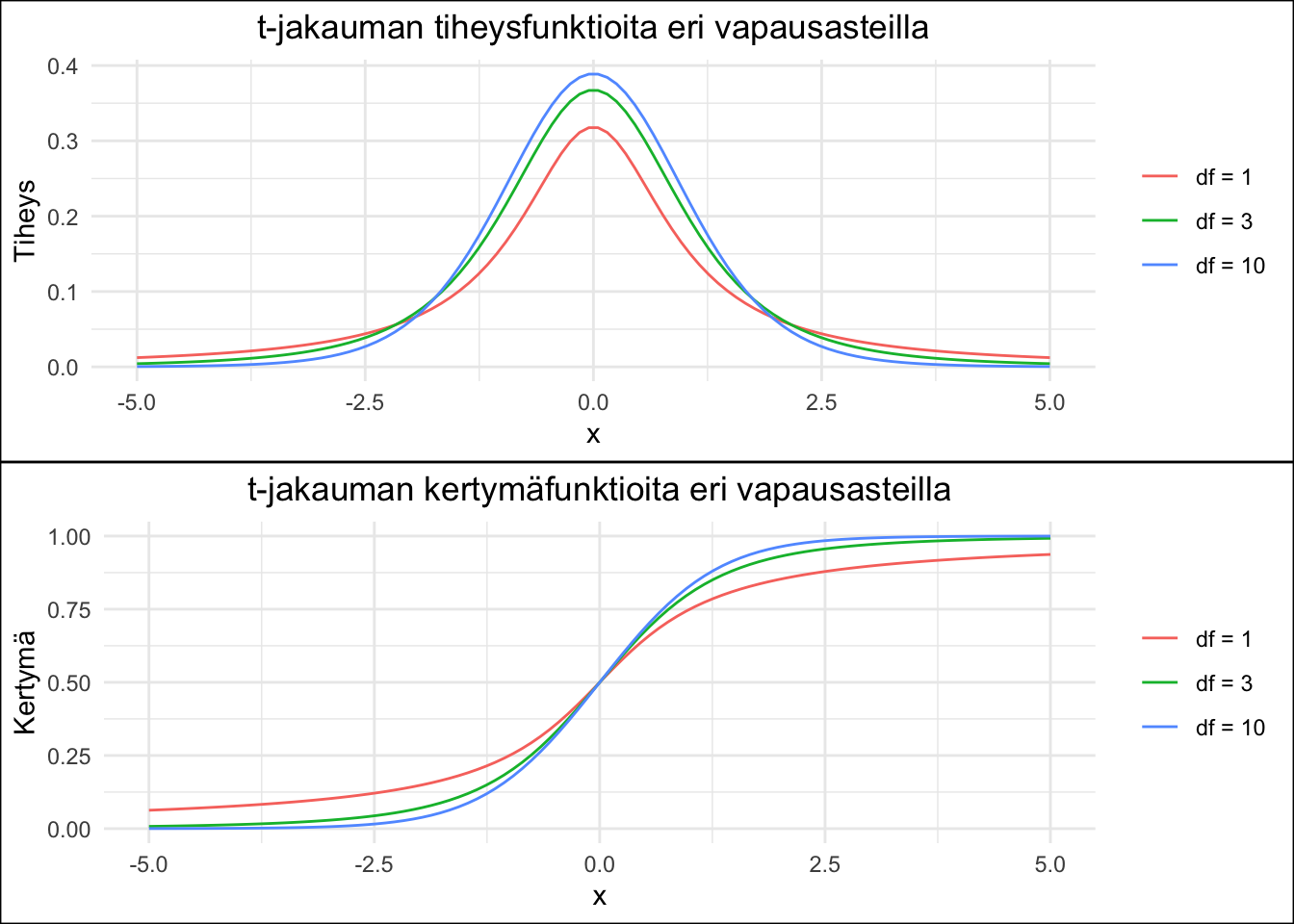
Figure 4.6: T-jakauman tiheys- ja kertymäfunktioita kolmella eri parametrillä.
