5 Moniulotteiset satunnaismuuttujat ja niiden jakaumat
Tässä kappaleessa tarkastellaan yksiulotteisen satunnaismuuttujan sijaan \(n\)-ulotteista satunnaisvektoria \(X=(X_1,X_2,...,X_n)\), joka koostuu yksiulotteisista satunnaismuuttujista. Moniulotteisen satunnaismuuttujan \(X\) käsitettä olisi myös mahdollista laajentaa satunnaismatriiseihin - ja siitä eteenpäinkin - mutta ne eivät kuulu tämän kurssin fokukseen.
Hyvin monet käytännön elämän ilmiöt ja aineistot ovat todellisuudessa moniulotteisia ja näiden tilastollis-teoreettiseen analyysiin ei yksiulotteiset keinot ole useinkaan riittäviä. Moniulotteisessa tilastollisessa analyysissä on tavoitteena tutkia esimerkiksi yksinkertaisia muuttujien riippuvuuksia toisistaan tai tiettyjen satunnaismuuttujien arvojen ennustamista toisista muuttujista. Moniulotteisen satunnaismuuttujan tapauksessa jotkin yksinkertaiset analyysit, esimerkiksi tavallisen odotusarvon lasku, ovat hyvin samankaltaisia kuin yksiulotteisessa tapauksessa. Pääsääntöisesti moniulotteisen muuttujan tilanteessa analyysi on kuitenkin monipuolisempaa, ja usein myös monimutkaisempaa ja siten myös vaativampaakin. Moniulotteisen satunnaismuuttujan tapauksessa on myös teoriaa ja käsitteitä, jota ei ole ollenkaan yksiulotteisen satunnaismuuttujan tapauksessa. Näiden ymmärtäminen ja soveltaminen vaativat selkeitä lisäaskelia yksiulotteisen satunnaismuuttujan analyysista, mutta toisaalta tarjoavat hyvin merkittäviä ja tärkeitä työkaluja niin teoreettiseen kuin puhtaan käytännölliseen analyysiin.
Diskreetti, jatkuva vai hybridi
Yksinkertaisissa tyyppitilanteissa moniulotteisen satunnaismuuttujan
kaikki elementit ovat joko diskreettejä tai jatkuvia. Varsin monissa
käytännön tilanteissa satunnaisvektori on luonteeltaan kuitenkin
hybridi: satunnaismuuttuja koostuu sekä diskreeteistä jatkuvista
satunnaismuuttujista (vaikkapa sukupuoli) että jatkuvista
satunnaismuuttujista (vaikkapa pituus). Tästä tyypillisestä
sekamuotoisuudesta huolimatta merkinnät ja muu taustateoria esitellään
yksinkertaisuuden vuoksi seuraavassa pelkästään diskreetille tai
jatkuvalle moniulotteiselle satunnaismuuttujalle. Perusteoria ja
käytäntö on hybriditilanteessa melko pitkälle samanlaista.
5.1 Yhteisjakauma ja sen merkinnöistä
Yksiulotteisen satunnaismuuttujan tapauksessa todennäköisyydet ja tilastolliset tunnusluvut saatiin laskettua satunnaismuuttujan (yksiulotteisesta jakaumasta): joko diskreetistä ptnf:stä tai jatkuvasta tiheysfunktiosta. Satunnaisvektorin tapauksessa vastaava primäärijakauma analyysille on yhteisjakauma. Tämä kertoo kaikkien satunnaisvektorin elementtien yhteisen jakauman, ja josta saadaan edelleen laskettua esimerkiksi todennäköisyyksiä saada satunnaisvektorin elementeille tietty arvo (diskreetti tapaus) tai tietty arvoväli (jatkuva tapaus). Huomaa, että termi ‘yhteisjakauma’ ei ota kantaa onko kyseessä diskreetti vai jatkuva satunnaismuuttuja
Yhteisjakaumalle käytetään erilaisia merkintöjä, mutta tämän kurssin puitteissa käytetään yhteisjakaumalle pääsääntöisesti pitkää merkintätapaa \(f_{Z,X}(z,x)\), jossa alaindeksissä luetellaan eksplisiittisesti yhteisjakauman satunnaismuuttujat (esimerkiksi \(Z\) ja \(X\)) ja funktion argumentteina on näitä vastaavat muuttujat (esimerkiksi \(z\) ja \(x\)). Tämä merkintä käy sekä diskreetille että jatkuvalle satunnaisvektorille. Lyhyempi merkintä yhteisjakaumalle on \(f(z,x)\) eli tässä ei tuoda selkeästi näkyviin funktion satunnaismuuttujia. Tässä materiaalissa käytetään lähtökohtaisesti pitkää merkintätapaa.
5.2 Diskreetti moniulotteinen satunnaisvektori
Satunnaisvektorin elementtien ollessa diskreettejä käytetään yhteisjakauman pistetodennäköisyyksille esimerkiksi merkintää \[p(x_1,x_2,...,x_n)=P(X_1=x_1, X_2=x_2,...,X_n=x_n),\] jossa \(p\)-merkintä korostaa pistetodennäköisyysluonnetta. Tällöin esimerkiksi kaksiulotteisen satunnaismuuttujan \(X=(X_1,X_2)\) yhteisjakaumalle \(f_{X_1,X_2}(x_1,x_2)\) käytetään merkintää \[p(x_1,x_2)=P(X_1=x_1, X_2=x_2),\] jossa funktio \(p\) kertoo pistetodennäköisyydet. Pistetodennäköisyydet voidaan edelleen ilmaista eksplisiittisesti pistetodennäköisyysfunktion kautta ja kaksiulotteisessa tapauksessa esimerkiksi taulukoituna tai mahdollisesti jopa kuvana.
Matemaattiset ehdot moniulotteisen diskreetin satunnaismuuttujan jakaumalle
- \(p(x_1,x_2,...,x_n) \geq 0\) (kaikki pistetodennäköisyydet oltava ei negatiivisia)
- \(\sum_{x_1,x_2,...,x_n}p(x_1,x_2,...,x_n)=1\) (todennäköisyyksien kokonaissumma = 1).
Nämä ehdot ovat vastaavat kuin aiemmin oli yksiulotteiselle satunnaismuuttujalle, mutta nyt vain moniulotteiseen tapaukseen sovellettuna.
Esimerkki 5.2.1
Kahden riippumattoman nopan \(N_1\) ja \(N_2\) muodostama
yhteis(todennäköisyys)jakauma
\[ \begin{array}{c|c|c|c|c|c|c} & N_1=1 & N_1=2 & N_1=3 & N_1=4 & N_1=5 & N_1=6 \\ \hline N_2=1 & 1/36 & 1/36 & 1/36 & 1/36 & 1/36 & 1/36 \\ N_2=2 & 1/36 & 1/36 & 1/36 & 1/36 & 1/36 & 1/36 \\ N_2=3 & 1/36 & 1/36 & 1/36 & 1/36 & 1/36 & 1/36 \\ N_2=4 & 1/36 & 1/36 & 1/36 & 1/36 & 1/36 & 1/36 \\ N_2=5 & 1/36 & 1/36 & 1/36 & 1/36 & 1/36 & 1/36 \\ N_2=6 & 1/36 & 1/36 & 1/36 & 1/36 & 1/36 & 1/36 \\ \end{array} \]
Esimerkki 5.2.2
Tutki muodostavatko seuraavat taulukoidut pistetodennäköisyydet
yhteisjakauman?
\[
\begin{array}{c|c|c|c|c|c}
& X_1=1 & X_1=2 & X_1=3 & X_1=4 & X_1=5 \\
\hline
X_2=1 & 3/125 & 4/125 & 5/125 & 6/125 & 5/125 \\
X_2=2 & 5/125 & 6/125 & 6/125 & 3/125 & 7/125 \\
X_2=3 & 2/125 & 1/125 & 8/125 & 8/125 & 6/125 \\
X_2=4 & 2/125 & 3/125 & 6/125 & 4/125 & 7/125 \\
X_2=5 & 3/125 & 4/125 & 6/125 & 7/125 & 8/125 \\
\end{array}
\]
Ratkaisu
Todennäköisyydet ovat selvästi ei-negatiivisia ja
summautuvat ykköseen. Näin ollen yo. taulukko kuvaa yhteisjakaumaa.
5.2.1 Kertymäfunktio diskreetissä tapauksessa
Kun satunnaismuuttujia on \(n\) kappaletta, niin diskreetin satunnaismuuttujan (yhteis)jakauman (yhteis)kertymäfunktio määritellään vastaavalla tavalla kertyneenä summana kuin yksiulotteisessa tapauksessa mutta nyt vain \(n\) muuttujan suhteen. Kahden diskreetin satunnaismuuttujan tapauksessa kertymäfunktio on \[F(x_1,x_2)=P(X_1\leq x_1, X_2 \leq x_2)=\sum_{u_1\leq x_1}\sum_{u_2\leq x_2}p(u_1,u_2),\] jossa \(p(u_1,u_2)\) kertoo pistetodennäköisyyden \(P(X_1=u_1, X_2=u_2)\).
Esimerkki 5.2.1.1
Määritä edellisen esimerkin kertymäfunktio ja määritä
tähän perustueen \(P(X_1 \leq 4,\, X_2 \leq 3)\).
Ratkaisu
Kertymäfunktio saadaan summaamalla taulukon pistetodennäköisyyksiä riveillä ja sarakkeilla edeten:
5.2.2 Multinomijakauma
Multinomijakauma on yksi paljon käytetty diskreetti moniulotteinen jakauma, joka on yleistys binomijakaumasta: kahden tapahtumavaihtoehdon sijasta on \(k>2\) vaihtoehtoa ja multinomijakaumassa tarkastellaan näiden näiden tapahtumien onnistumisten lukumäärää yhteisjakauman mielessä. Määritellään, että \(X_i\) on tapahtuman \(i\) onnistumisten lukumäärä \(n\)-kertaisessa riippumattomassa toistokokeessa. Oletetaan, että kokeessa tarkastellaan \(k\):ta erillistä tapahtumaa, joista kukin esiintyy \(n_1, \ldots, n_k\) kertaa siten, että tapahtumien summalle pätee \(\sum_{i=1}^k n_i = n\). Lisäksi oletetaan, että tapahtumien onnistumistodennäköisyydet ovat \(p_1, \ldots, p_k\), joille pätee \(\sum_{i=1}^k p_i = 1\). Tällöin yhteisjakauma \((X_1,\ldots,X_k)\) on jakautunut multinomiaalisesti skalaariparametrillä \(n\) ja vektoriparametrillä \(p=(p_1,\ldots ,p_k)\). Jakautumismerkintänä tälle käytetään esimerkiksi \(X \sim Mult(n,p),\) mutta kirjallisuudessa on myös muita merkintätapoja tälle. Lisätietoa multinomijakaumasta ja sen käytöstä löytyy täältä.
Multinomijakauman pistetodennäköisyysfunktio: \[P(X_1=n_1,\ldots , X_k=n_k)=\frac{n!}{n_1! \cdots n_k!}p_1^{n_1}\cdots p_k^{n_k}=\frac{n!}{\Pi_{i=1}^kn_i!}\Pi_{i=1}^np_i^{n_i}.\]
5.2.2.1 Multinomikerroin
Multinomijakauman termiä \(\frac{n!}{n_1! \cdots n_k!}\) sanotaan *multinomikertoimeksi* ja se kertoo kuinka monella tavalla \(n\):n kokoinen joukko voidaan jakaa \(k\):hon osajoukkoon, joiden koot ovat \(n_1,\ldots,n_k\) ja joille \(\sum_{i=1}^kn_i=n.\) Nyt esimerkiksi 10 hengen kokoinen ryhmä voidaan jakaa kolmeen ryhmään, joiden koot ovat \(5,3\) ja \(2\) henkeä \(\frac{10!}{5!3!2!}=2520\) tavalla.
5.2.2.2 Multinomijakauman ominaisuuksia
Kun \((X_i,\ldots,X_n)\sim Mult(n,p)\), niin
- Odotusarvo: \(E(X_i)=np_i\)
- Varanssi: \(Var(X_i)=np_i(1-p_i)\)
- Kovarianssi: \(Cov(X_i,X_j)=-np_ip_j, \text { kun } i\neq j\)
Lisäksi
- Kun multinomijakaumassa \(k=2\) ja \(n>1\), niin multinomijakauma on binomijakauma
- Kun multinomijakaumassa \(k=2\) ja \(n=1\), niin multinomijakauma on oleellisesti bernoullijakauma
Esimerkki 5.2.2.1
Karkkirasiassa on kolmea eri karkkilajiketta, joiden suhteellinen
valmistusosuus on tehtaalla: mansikkakarkki \(p_1 = 0.3\),
mustikkakarkki \(p_2 = 0.25\), salmiakki \(p_3 = 0.45\). Mikä on
todennäköisyys, että kymmenen karkin rasiassa on kaksi mansikkaa, kolme
mustikkaa ja viisi salmiakkia?
Ratkaisu
Nyt \(k=3\), todennäköisyydet ovat \(p_1 = 0.3\),
\(p_2 = 0.25\), \(p_3 = 0.45\) ja lukumäärät \(n_1 = 2\), \(n_2 = 3\),
\(n_3 = 5\) jolloin \(\sum n_i = 10\). Multinomijakauman pistetodennäköisyysfunktion
mukaan kysytty todennäköisyys on
\(\frac{n!}{\Pi_{i=1}^kn_i!}\Pi_{i=1}^np_i^{n_i}=\frac{n!}{n_1!n_2!n_3!}{p_{1}}^{n_1}\cdot
{p_{2}}^{n_2}\cdot {p_{2}}^{n_3}\) \(=\frac{10!}{2!\cdot3!\cdot5!}0.3^{2}\cdot
0.25^{3}\cdot 0.45^{5}=0.0654\).
5.3 Jatkuva moniulotteinen satunnaismuuttuja
Satunnaisvektorin elementtien ollessa jatkuvia kertoo yhteistiheysfunktio \(f\) todennäköisyyden kertymisen vauhdin vastaavalla tavalla kuin yksiulotteisessa tilanteessa.
Matemaattiset ehdot moniulotteisen jatkuvan satunnaismuuttujan jakaumalle
- \(f(x_1,x_2,...,x_n) \geq 0\) (tiheysfunktion arvot ovat ei-negatiivisia)
- \(\int_{-\infty}^\infty \int_{-\infty}^\infty ...\int_{-\infty}^\infty f_{X_1,X_2...,X_n}(x_1,x_2,...,x_n)dx_1 dx_2 \cdots dx_n= 1\) (kokonaisintegraali = 1)
Esimerkki 5.3.1
Yritys mallintaa kahden prosessinsa odotusaikojen yhteisjakaumaa funktiolla
\(h(t_1,t_2)=21e^{-(3t_1+7t_2)}\), kun \(t_1,t_2 \geq 0\) ja nolla
muutoin. Tutki täyttääkö funktio yhteistiheyden ehdot?
Ratkaisu
Määrittelyvälillään funktio on selvästi
ei-negatiivinen. Lasketaan seuraavaksi integraali
\(\int_{0}^{\infty} \int_{0}^{\infty} 21e^{-(3t_1+7t_2)}dt_1
dt_2\). Aloitetaan integrointi sisältä muuttujan \(t_1\) suhteen,
jolloin integraalista saadaan \(\int_{0}^\infty
21e^{-7t_2}\left(\int_{0}^{\infty} e^{-3t_1}dt_1 \right)dt_2\).
Koska sisäintegraali \(\int_{0}^{\infty} e^{-3t_1}dt_1={\huge
|}_0^{\infty} \frac{e^{-3t_1}}{-3} = \frac{1}{3}\) saadaan
alkuperäiseksi integraaliksi siis \(\int_{0}^{\infty} 21e^{-7t_2}
\frac{1}{3} dt_2=\int_{0}^{\infty} -\frac{21}{7\cdot 3}e^{-7t_2}=0-(-1)=1\).
Funktio \(h\) täyttää siis (yhteis)tiheysfunktion ehdot.
5.3.1 Kertymäfunktio jatkuvassa tapauksessa
Jatkuvan satunnaismuuttujan kertymäfunktio saadaan vastaavalla tavalla määrittämällä kertymä määrätyn integraalin avulla \(F(x)=\int_{-\infty}^{x}f(x)dx\) jossa \(x\) tulkitaan tässä moniulotteisena. Jatkuvan kaksiulotteisen satunnaismuuttujan (yhteis)kertymäfunktio voidaan näin ollen kirjoittaa muotoon \[F(x_1,x_2)=\int_{-\infty}^{x_1} \int_{-\infty}^{x_2}f(u_1,u_2)du_1 du_2,\] jossa \(f(u_1,u_2)\) kertoo yhteistiheysfunktion arvon kohdassa \(X_1=u_1, X_2=u_2\). Kolmi- ja useampiulotteiset jatkuvat yhteisjakaumat voidaan määritellä aivan vastaavalla tavalla.
Esimerkki 5.3.1.2
Laske edellisen tehtävän tiheysfunktioon perustuen
\(P(0.1 \leq T_1\leq 0.6, 0.1\leq T_2\leq 0.4)\).
Ratkaisu
Kysytty todennäköisyys saadaan nyt integraalina
\(\int_{0.1}^{0.4} \int_{0.1}^{0.6} 21e^{-(3t_1+7t_2)}dt_1
dt_2\). Aloitetaan integrointi sisältä muuttujan \(t_1\) suhteen,
jolloin integraalista saadaan
\(\int_{0.1}^{0.4}21e^{-7t_2}\left(\int_{0.1}^{0.6}
e^{-3t_1}dt_1 \right)dt_2\). Koska sisäintegraali
\(\int_{0.1}^{0.6} e^{-3t_1}dt_1={\huge |}_{0.1}^{0.6}
\frac{e^{-3t_1}}{-3} = \frac{e^{-0.3}-e^{-1.8}}{3}\) saadaan
alkuperäiseksi integraaliksi siis \(\frac{e^{-0.3}-e^{-1.8}}{3}
\int_{0.1}^{0.4} 21e^{-7t_2}
dt_2=\frac{e^{-0.3}-e^{-1.8}}{3}\frac{21}{7}(e^{-0.7}-e^{-2.8})\).
5.3.2 Moniulotteinen normaalijakauma
Kuten aiemmin todettiin, on normaalijakaumalla tärkeä rooli selittää monitekijäisiä havaintoja. Sama pätee myös moniulotteiseen tilanteeseen ja moniulotteinen normaalijakauma on yksi eniten käytetyistä jakaumamalleista moniulotteisen satunnaismuuttujan tapauksessa. Moniulotteinen satunnaismuuttuja \(X=(X_1, ..., X_n)\) noudattaa \(n\)-ulotteista normaalijakaumaa jos yhteisjakauman tiheysfunktio on seuraavaa muotoa
Moniulotteisen normaalijakauman tiheysfunktio \[f_{X}(x)=\frac{exp\left( -\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)}{\sqrt{\|2\pi \Sigma\|}},\] jossa \(\mu=(E(X_1),E(X_2), ..., E(X_n))\) on \(n\)-ulotteisen satunnaismuuttujan \(X\):n odotusarvovektori ja \(\Sigma\) on muuttujien kovarianssimatriisi, joka on \(n \times n\) matriisi koostuen elementeistä \(\Sigma_{ij}=Cov(X_i,X_j)\), ja jossa merkintä \(\| \cdot\|\) tarkoittaa matriisin determinantin laskua.
Tyypillisiä merkintöjä moniulotteiselle normaalijakautumiselle ovat \(X \sim N(\mu,\Sigma)\), \(X \sim MNorm(\mu, \Sigma)\) tai \(X \sim Multinorm (\mu,\Sigma)\).
5.3.2.1 Moniulotteisen normaalijakauman erityisominaisuus
Moniulotteisella normaalijakaumalla on seuraava erityisominaisuus: korreloimattomuudesta seuraa riippumattomuus. Tämä ominaisuus on tavallisuudesta poikkeava, sillä yleisesti ottaen on siis voimassa vain “riippumattomuus \(\Rightarrow\) korreloimattomuus”. Moniulotteisen normaalijakauman tapauksessa implikaatio on siis myös toiseen suuntaan. Tämä on yksi normaalijakauman hyödyllisistä ominaisuuksista.
5.3.3 Kaksiulotteinen normaalijakauma
Kaksiulotteisen normaalijakauman tiheysfunktio \[f_{X_1,X_2}(x_1,x_2)=\frac{exp\left( -\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)}{\sqrt{\|2\pi \Sigma\|}},\] jossa \(\mu=(E(X_1),E(X_2))\) on \(X\):n odotusarvovektori.
Kaksiulotteisen normaalijakauman tapauksessa kovarianssimatriisi \(\Sigma\) on \[ \Sigma=\left[ \begin{array}{cc} \sigma_1^2 & \rho \sigma_1\sigma_2 \\ \rho \sigma_1\sigma_2 & \sigma_2^2 \end{array} \right], \] koostuen \(X_i\):n varianssista \(\sigma_i^2\) sekä muuttujien \(X_1\) ja \(X_2\) välisestä korrelaatiokertoimesta \(\rho=Cov(X_1,X_2)/\sqrt{Var(X_1)Var(X_2)}\). Kaksiulotteiselle normaalijakautumiselle voidaan käyttää myös merkintää tai \(X \sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)\) jossa tuodaan kaikki jakauman määräävät parametrit eksplisiittisesti mukaan parametrisointiin geneerisen \(\Sigma\)-merkinnän sijaan.
Esimerkki 5.3.3.1
Laske todennäköisyys \(P(X_1 \leq 0\), \(X_2 \leq 1)\), kun
\((X_1,X_2)\) noudattaa kaksiulotteista standardinormaalijakaumaa.
Ratkaisu
Todennäköisyys saadaan integraalista
\(\int_{-\infty}^{0} \int_{-\infty}^{1}
f_{X_1,X_2}(x_1,x_2)dx1_dx_2\), jossa \(f_{X_1,X_2}(x_1,x_2)\) on
kaksiulotteisen standardinormaalijakauman tiheysfunktio. Koska
kaksiulotteisen standardinormaalijakauman odotusarvo on \(\mu=(0,0)\) ja
kovarianssimatriisi on \[ \Sigma=\left[ \begin{array}{cc} 1 & 0
\\ 0 & 1 \end{array} \right] \] voidaan integraali kirjoittaa
muotoon \[ \frac{1}{\sqrt{2\pi}}
\int_{-\infty}^{0}exp\left(-\frac{x_1^2}{2}\right)dx_1
\frac{1}{\sqrt{2\pi}}
\int_{-\infty}^{1}exp\left(-\frac{x_2^2}{2}\right)dx_2.\]
R-komennoilla pnorm(0,mean=0,sd=1) ja pnorm(1,mean=0,sd=1)saadaan
lukuarvot integraaleille \(\frac{1}{\sqrt{2\pi}}
\int_{-\infty}^{0}exp\left(-\frac{z^2}{2}\right)dz=0.5\) ja
\(\frac{1}{\sqrt{2\pi}}
\int_{-\infty}^{1}exp\left(-\frac{z^2}{2}\right)dz=0.8413\).
Kyseiset integraalin arvot löytää myös perinteisistä standardinormaalijakauman taulukoista.
Lopputulokseksi saadaan siis \(P(X_1 \leq 0, X_2 \leq 1)=0.5\cdot0.8413=0.4206\).
5.3.4 Tasa-arvokäyrät kaksiulotteiselle normaalijakaumalle
Kaksiulotteisen satunnaismuuttujan tiheysfunktiolle voidaan määritellä tasa-arvokäyrät, jotka muodostuvat niistä satunnaismuuttujan arvojen pisteistä, joilla yhteistiheyden arvot ovat samoja (ks. lisää tasa-arvokäyristä täältä). Käytännön analogiana tasa-arvokäyrille on maastokarttojen korkeuskäyrät, jotka muodostuvat samalla korkeudella maanpinnasta olevista pisteistä. Kaksiulotteisella normaalijakaumalla tasa-arvokäyrät ovat ellipsejä, joiden keskipisteenä on odotusarvo \(\mu=(E(X),E(Y))\) ja joiden muoto riippuu kovarianssimatriisista eli variansseista ja korrelaatiokertoimesta.
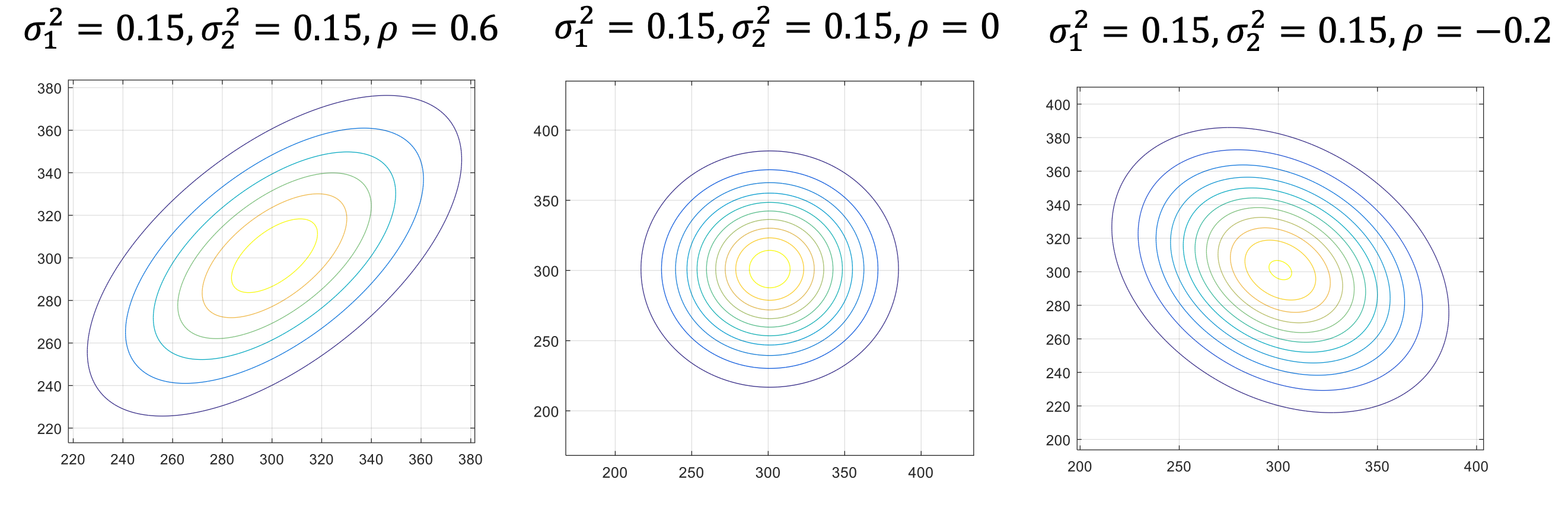
Figure 5.1: Kaksiulotteisen normaalijakauman tasa-arvokäyriä eri kovarianssirakenteilla.
5.4 Marginaali- eli reunajakaumat
Moniulotteiset jakaumat kertovat satunnaismuuttujien yhteisjakaumasta kaikkien tarkasteltavien satunnaismuuttujien suhteen. Joskus on kuitenkin tarpeen tarkastella jakaumaa, jossa on vähemmän muuttujia. Tämä tehdään marginalisoimalla ylimääräiset tai tarkastelun suhteen ei-kiinnostavat muuttujat pois: kun alkuperäinen yhteisjakauma on esimerkiksi kaksiulotteiselle satunnaismuuttujalle \((X,Y)\), niin marginalisoimalla yhteisjakaumasta muuttuja \(X\) pois saadaan \(Y\):n jakauma, jota kutsutaan alkuperäisen jakauman marginaalijakaumaksi tai reunajakaumaksi. Marginalisointi toteutetaan eri tavoin riippuen marginalisoitavien satunnaismuuttujien luonteesta. Marginalisoinnin luonteesta riippumatta saatu marginaalijakauma on edelleen todennäköisyysjakauma, jolle pätee normaalit jakauman matemaattiset ehdot.
5.4.1 Marginaalijakaumat diskreetissä tapauksessa
Marginalisointi diskreettien satunnaismuuttujien tapauksessa tehdään summaamalla yli marginalisoitavien satunnaismuuttujien. Jos esimerkiksi diskreetistä yhteisjakaumasta \(f_{X,Y}(x,y)=P(X=x, Y=y)\) halutaan selvittää \(Y\):n marginaalijakauma \(f_Y(y)=P(Y=y)\), niin se saadaan summaamalla yli marginalisoitavan muuttujan \(X\) mahdollisten arvojen \[f_Y(y)=\sum_{x}f_{X,Y}(x,y).\]
Vastaavasti kolmiulotteisesta diskreetistä yhteisjakaumasta \(f_{X,Y,Z}(x,y,z)=P(X=x, Y=y, Z=z)\) saadaan seuraavat yksiulotteiset diskreetit marginaalijakaumat summaamalla yli irrelevanttien muuttujien
\[f_X(x)=\sum_{z}\sum_{y}f_{X,Y,Z}(x,y,z)\] \[f_Y(y)=\sum_{x}\sum_{z}f_{X,Y,Z}(x,y,z)\] \[f_Z(z)=\sum_{x}\sum_{y}f_{X,Y,Z}(x,y,z)\]
Esimerkki 5.4.1.1
Laske ao. taulukon mukaisen yhteisjakauman reunajakaumat
\[
\begin{array}{c|c|c|c|c|c}
& X_1=1 & X_1=2 & X_1=3 & X_1=4 & X_5=5 \\
\hline
X_2=1 & 3/125 & 4/125 & 5/125 & 6/125 & 5/125 \\
X_2=2 & 5/125 & 6/125 & 6/125 & 3/125 & 7/125 \\
X_2=3 & 2/125 & 1/125 & 8/125 & 8/125 & 6/125 \\
X_2=4 & 2/125 & 3/125 & 6/125 & 4/125 & 7/125 \\
X_2=5 & 3/125 & 4/125 & 6/125 & 7/125 & 8/125 \\
\end{array}
\]
Ratkaisu
Marginaalijakauma \(X_1\):n suhteen saadaan summaamalla yli muuttujan
\(X_2\) mahdollisten arvojen (eli tässä tapauksessa laskemalla
sarakesumma). Reunajakauma \(X_1\) on siis \[
\begin{array}{\|c\|c\|c\|c\|c\|} X_1 = 1 & X_1 = 2 & X_1 = 3 & X_1 = 4 & X_1=5
\\\hline \frac{15}{125} &
\frac{18}{125}&\frac{31}{125}&\frac{28}{125}&\frac{33}{125} \end{array} \]
Vastaavasti marginaalijakauma \(X_2\) suhteen saadaan analogisesti (laskemalla rivisummat): \[ \begin{array}{\|c\|c\|c\|c\|c\|c\|} X_2 = 1 & X_2 = 2 & X_2 = 3 & X_2 = 4 & X_2 = 5\\\hline \frac{23}{125}&\frac{27}{125}&\frac{25}{125}&\frac{22}{125}&\frac{28}{125} \end{array}. \] Kumpikin marginaalijakauma täyttää selvästi ptnf:n ehdot (positiivisia ja summautuu ykköseen).
Esimerkki 5.4.1.2
Oletetaan seuraava kaksiulotteinen diskreetti ptnf \[ f_{X,Z}(x,z) =
\begin{cases} \frac{1}{8}\left(1+\frac{z}{3}\right)\frac{1}{14},
\text{ kun } x=0,1,...,7 \text{ ja } z=0,1,...,6\\ 0, \qquad
\qquad \qquad \quad \, \, \, \text{muualla} \end{cases} \]
Määritä tämän jakauman reunajakaumat.
Ratkaisu
Reunajakauma \(f_X(x)\) saadaan summaamalla ptnf yli
muuttujan \(Z\) mahdollisten arvojen:
\[ f_X(x) = \sum_{z=0}^{6} \frac{1}{8}\left(1+\frac{z}{3}\right)\frac{1}{14} \\ \frac{1}{14}\frac{1}{8} \sum_{z=0}^{6} \left(1+\frac{z}{3}\right)= \\ \frac{1}{14}\frac{1}{8}*\left( 1+\frac{0}{3}+ 1+\frac{1}{3} + 1+\frac{2}{3} + 1+\frac{3}{3} + 1+\frac{4}{3} + 1+\frac{5}{3} + 1+\frac{6}{3} \right) = \\ \frac{1}{14}\frac{1}{8}\cdot\left( 7+ \frac{1+2+3+4+5+6}{3} \right) = \frac{1}{14}\frac{1}{8}\cdot 14 = \frac{1}{8}\] Nyt siis \(f_X(x) = \frac{1}{8}\), kun \(x=0,1,...,7\).
Vastaavasti reunajakauma \(f_Z(z)\) saadaan summaamalla ptnf yli muuttujan \(X\) mahdollisten arvojen:
\[ f_Z(z) = \sum_{x=0}^{7} \frac{1}{8}\left(1+\frac{z}{3}\right)\frac{1}{14} = 8* \frac{1}{8}\left(1+\frac{z}{3}\right)\frac{1}{14} =\frac{1}{14}\left(1+\frac{z}{3}\right)\]
Nyt siis \(f_Z(z) = \frac{1}{14}\left(1+\frac{z}{3}\right)\), kun \(z=0,1,...,6\). Kummallekin lasketulle reunajakaumalle pätee jakaumien perusehdot: ei-negatiivisuus ja summautuvat ykköseen (itsenäinen harjoitus).
5.4.2 Marginaalijakaumat jatkuvassa tapauksessa
Marginalisointi jatkuvien satunnaismuuttujien tapauksessa tehdään integroimalla yli marginalisoitavien satunnaismuuttujien. Jos esimerkiksi tiheysfunktiosta \(f_{X,Y}(x,y)\) halutaan selvittää \(Y\):n marginaalijakauma (eli reunatiheys) \(f_Y(y)\), niin se saadaan integroimalla yli marginalisoitavan muuttujan \(X\) mahdollisten arvojen. Kaksiulotteisesta yhteisjakaumasta \(f_{X,Y}(x,y)\) saadaan laskettua esimerkiksi marginaalijakauma \[f_Y(y)=\int_{x}f_{X,Y}(x,y)dx.\]
Vastaavasti kolmiulotteisesta yhteisjakaumasta \(f_{X,Y,Z}(x,y,z)\) saadaan seuraavat yksiulotteiset jatkuvat marginaalijakaumat
\[f_X(x)=\int_{z}\int_{y}f_{X,Y,Z}(x,y,z)dydz\] \[f_Y(y)=\int_{x}\int_{z}f_{X,Y,Z}(x,y,z)dzdx\] \[f_Z(z)=\int_{x}\int_{y}f_{X,Y,Z}(x,y,z)dydx\]
Käytännön marginaalijakauman laskuissa joudutaan lähes aina käyttämään integrointitaitoja tai ulkoisia työkaluja symboliseen tai numeeriseen integrointiin.
Esimerkki 5.4.2.1
Oletetaan,
että jatkuvat satunnaismuuttujat \(X\) ja \(Y\) noudattavat
(yhteis)tiheysfunktiota \(f(x,y)=e^{-y}, \text{ kun }
0 <x <y <\infty\). Määritä \(X\):n marginaalijakauma.
Ratkaisu
Ensimmäiseksi huomataan tiheysfunktiosta, että satunnaismuuttuja X
esiintyy alarajana Y:lle, mutta ei varsinaisesti funktiolausekkeen “sisällä”.
Aiemman perusteella saadaan marginaalijakauma saadaan laskettua integraalina
\(f_X(x)=\int_{-\infty}^{\infty}f_{X,Y}(x,y)dy=\int_{x}^{\infty}e^{-y}dy\).
Soveltamalla tähän
perusintegrointikaavoja
saadaan marginaalijakaumaksi
\(f_X(x)=\int_{x}^{\infty}e^{-y}dy=0-(-e^{-x})dy=e^{-x}\).
Lisähuomio: lasketun tuloksen funktionaalisesta muodosta todetaan, että ylläolevan yhteistiheyden marginaalijakauma \(X\):n suhteen eli reunatiheys \(f_X(x)\) on eksponenttijakauma parametrilla
\(1\) eli \(X \sim Exp(1)\).
Esimerkki 5.4.2.2
Oletetaan,
että jatkuvat satunnaismuuttujat \(X\) ja \(Z\) noudattavat
(yhteis)tiheysfunktiota \(f(x,z) = \frac{x}{12} \frac{2+z}{20}\), kun
\(1 \leq x \leq 5\) ja \(1 \leq z \leq 5\) Määritä marginaalijakauma
\(X\):n suhteen.
Ratkaisu
Aiemman mukaan \[f_X(x) = \int_{-\infty}^{\infty} \frac{x}{12}
\frac{2+z}{20}dz = \\ \int_{1}^{5} \frac{x}{12} \frac{2+z}{20}dz
= \frac{x}{12} {\huge |}_{1}^{5} \frac{1}{20} \left(
\frac{z^2}{2} +2z \right) = \\ \frac{x}{12} \cdot \frac{1}{20}
\left( \frac{5^2}{2} +2\cdot5 - \frac{1^2}{2} -2\cdot1 \right) =\\
\frac{x}{12\cdot20} \left( \frac{25}{2} +10 - \frac{1}{2} -2 \right) =
\frac{x}{12}. \\ \] Marginaalijakaumaksi saadaan siis \(f_X(x) =
\frac{x}{12}\), kun \(1 \leq x \leq 5\). Matemaattisten jakaumaehtojen tarkistus
tälle on suoraviivainen lasku (kokeile itse).
Esimerkki 5.4.2.3
Oletetaan, että \(X\):n ja \(Y\):n yhteistiheys noudattaa jakaumaa
\(f_{XY}(x,y)=2\), kun \(0 <x <y <1\). Määritä reunajakaumat.
Ratkaisu
Nyt marginaalifunktio \(f_x(x)\) saadaan integroimalla yli \(y\):n ja käyttämällä tehtävässä annettuja rajoja \(y\):lle. Näin ollen \(f_x(x)=\int_x^1 2dy= 2-2x\), kun \(0<x<1\) ja
vastaavasti \(f_Y(y)=\int_0^y 2dx= 2y\), kun \(0<y<1\).
5.4.2.1 Kaksiulotteisen normaalijakauman marginaalijakaumat
Kaksiulotteisen normaalijakauman \[f_{X_1,X_2}(x_1,x_2)=\frac{exp\left( -\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)}{\sqrt{\|2\pi \Sigma\|}}\] marginaalijakaumat ovat \[f_{X_1}(x_1)=(\sigma_1\sqrt{2\pi})^{-1}exp\left(-\frac{(x_1-\mu_1)^2}{2\sigma_1^2}\right)\] \[f_{X_2}(x_2)=(\sigma_2\sqrt{2\pi})^{-1}exp\left(-\frac{(x_2-\mu_2)^2}{2\sigma_2^2}\right).\]
Saadut marginaalijakaumat ovat siis normaalisia eivätkä riipu mitenkään mahdollisesta korrelaatiokertoimesta \(\rho\) kovarianssimatriisin \(\Sigma\) sisällä. Vastaava tulos pätee myös yleisemminkin: moniulotteisen normaalijakauman marginaalijakaumat ovat normaalisia
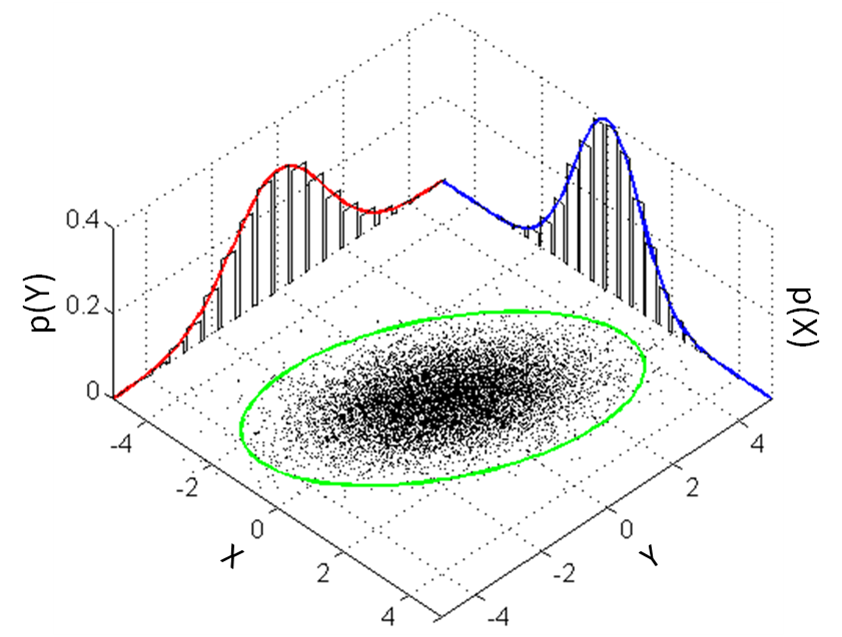
Figure 5.2: Kaksiulotteisen normaalijakauman marginaalijakaumat
5.5 Satunnaismuuttujien riippuvuus tai riippumattomuus
Yleisesti ottaen ei voida koskaan tehdä automaattista oletusta, että yhteisjakauman muuttujat olisivat riippumattomia. Lähtökohtaisesti kannattaakin olettaa, että yhteisjakauman muuttujat ovat jollakin tavalla riippuvia, ellei muuta parempaa tietoa ole käytettävissä. Riippuvuutta tai riippumattomuutta voidaan selvittää paremmin tutkimalla yhteisjakaumaa, josta joskus nähdään “suoraan” riippuvuus tai riippumattomuus - ja joskus tämä pitää selvittää laskulla tarkemmin. Riippumattomuuden selvittämiseen voidaan käyttää aiemmista opinnoista tuttua todennäköisyyksien riippumattomuusehtoa (riippumattomille \(P(A \text{ ja } B)=P(A)*P(B)\)) joka voidaan kirjoittaa aivan vastaavasti jakaumille:
Riippumattomuusehto: jos yhteisjakauma voidaan kirjoittaa tulona yksittäisten satunnaismuuttujien jakaumista ovat satunnaismuuttujat riippumattomia eli jos seuraava ehto pätee \[f_{X_1,X_2,...,X_n}(x_1,x_2,...,x_n)=\prod_i f_{X_i}(x_i).\]
Nyt riippumattomuusehto esimerkiksi kahden satunnaismuuttujan tapauksessa on muotoa \[f_{XY}(x,y)=f_{X}(x)f_{Y}(y)\] eli jos yhteisjakauma \(f_{XY}(x,y)\) voidaan kertoa ehdottomien (marginaali)jakaumien \(f_{X}(x)\) ja \(f_{Y}(y)\) tulona, niin muuttujat ovat riippumattomia. Mikäli näin ei ole, niin muuttujat eivät ole riippumattomia.
Edellisen riippumattomuuden lisäksi moniulotteisen satunnaismuuttujan tapauksessa on olemassa ehdollisen riippumattomuuden käsite. Tätä ei kuitenkaan käsitellä tällä kurssilla.
Esimerkki 5.5.1
Tutki onko yhteysjakauman
\[
f_{X,Y}(x,y) =
\begin{cases}
\frac{4}{5}(1 + xy), & \text{kun } 0 \le x \le 1 \text{ ja } 0 \le y \le 1 \\
0, & \text{muulloin}
\end{cases}
\]
satunnaismuuttujat riippumattomia.
Ratkaisu
Lasketaan aluksi marginaalijakaumat \(f_X(x)\) ja \(f_Y(y)\)
Marginaalijakaumiksi saadaan integrointien jälkeen (tarkista itse)
\(f_X(x)=\frac{4+2x}{5}\), kun \(0\leq x\leq 1\) ja
\(f_Y(y)=\frac{4+2y}{5}\), kun \(0\leq y\leq 1\).
Selvästikään marginaalijakaumien tulo \(f_X(x)f_Y(y)\) ei ole sama kuin yhteisjakauma. Näin ollen muuttujat eivät ole riippumattomia.
5.6 Tilastollisia tunnuslukuja moniulotteisille satunnaismuuttujille
Moniulotteisen satunnaismuuttujan tapauksessa tilastollisten tunnuslukujen lasku on pääosin moniulotteisempaa ja rikkaampaa kuin yksiulotteisen satunnaismuuttujan tapauksessa. Seuraavassa käydään läpi muutamia perustunnuslukuja. Näiden lisäksi moniulotteisille satunnaismuuttujille on olemassa muita eksoottisempia tunnuslukuja, jotka kuitenkin jätetään tämän kurssin ulkopuolelle.
5.6.1 Satunnaisvektorin odotusarvo
Moniulotteisen satunnaisvektorin odotusarvo saadaan laskemalla yksittäisten satunnaismuuttujien odotusarvot vastaavalla tavalla kuin aiemmin: painottamalla mahdollisia tulosvaihtoehtoja ko. satunnaismuuttujan marginaalijakaumalla eli marginaalitodennäköisyyksillä tai marginaalitiheydellä.
Moniulotteiset odotusarvot \[\mu_i=E(X_i)=\sum_{x_i} x_if_{X_i}(x_i) \text{(diskreetti tapaus) }\] \[\mu_i=E(X_i)=\int x_i f_{X_i}(x_i)dx_i \text{ (jatkuva tapaus) }\]
Vaihtoehtoisesti ylläolevat odotusarvot voi laskea käyttäen yhteisjakaumaa, jolloin \[\mu_i=\sum_{x_1,x_2,...,x_n} x_i f_{X_1,X_2...,X_n}(x_1,x_2...,x_n) \text{(diskreetti tapaus) }\] \[\mu_i=\int_{-\infty}^\infty \int_{-\infty}^\infty ...\int_{-\infty}^\infty x_i f_{X_1,X_2...,X_n}(x_1,x_2,...,x_n)dx_1dx_2\cdots dx_n.\]5.6.1.1 Moniulotteisen satunnaismuuttujan muunnoksen odotusarvo
Joskus ollaan kiinnostuneita myös odotusarvosta, kun satunnaismuuttujiin kohdistetaan joku
funktio \(g\). Käytännön esimerkkinä funktio \(g\) voisi esimerkiksi olla satunnaismuuttujien tulo, joka kertoo satunnaismuuttujat \(myyntihinta\) ja \(lukumäärä\) keskenään, jolloin lasketaan odotusarvoa myyntituloista.
Kahden satunnaismuuttujan ja funktion g tapauksessa odotusarvo voidaan laskea seuraavasti
\[E(g(X,Y))=\sum_x\sum_y g(x,y)f_{X,Y}(x,y) \text{ (diskreetti tapaus) }\]
\[E(g(X,Y))=\int_x\int_y g(x,y)f_{X,Y}(x,y)dydx \text{ (jatkuva tapaus) }\]
Esimerkki 5.6.1.1
Oletetaan seuraava diskreetti yhteisjakauma
\[
\begin{array}{c|c|c}
\hline
& X_1=1& X_1=2 \\ \hline
X_2=3 & \frac{3}{18} & \frac{4}{18} \\ \hline
X_2=4 & \frac{5}{18} & \frac{6}{18} \\ \hline
\end{array}.
\]
Laske odotusarvovektorit \((E(X_1),E(X_2))\) sekä \((E(X_1^2),E(X_2^2))\) .
Ratkaisu
Lasketetaan odotusarvot käyttäen yhteisjakaumaa:
\(E(X_1)=1\cdot\frac{3}{18}+1\cdot\frac{5}{18}+2\cdot\frac{4}{18}+2\cdot\frac{6}{18}=\frac{28}{18}\),
\(E(X_2)=3\cdot\frac{3}{18}+3\cdot\frac{4}{18}+4\cdot\frac{5}{18}+4\cdot\frac{6}{18}=\frac{65}{18}\),
\(E(X_1^2)=1^2\cdot\frac{3}{18}+1^2\cdot\frac{5}{18}+2^2\cdot\frac{4}{18}+2^2\cdot\frac{6}{18}=\frac{48}{18}\),
\(E(X_2^2)=3^2\cdot\frac{3}{18}+3^2\cdot\frac{4}{18}+4^2\cdot\frac{5}{18}+4^2\cdot\frac{6}{18}=\frac{239}{18}\).
Samaan lopputulokseen päädytään laskemalla ensin muuttujien
yksiulotteiset marginaalijakamat ja laskemalla vastaavat odotusarvot
näitä hyödyntämällä (tarkista itse).
Esimerkki 5.6.1.2 (jatkoa edelliselle esimerkille)
Laske odotusarvo
suureelle \(Z=X_1+X_2\).
Ratkaisu
Muunnosfunktio on nyt \(g(x,y)=x+y\) ja kysytty odotusarvo on nyt
\(E(X_1+X_2)=(3+1)\cdot\frac{3}{18}+(3+2)\cdot\frac{4}{18}+(4+1)\cdot\frac{5}{18}+(4+2)\cdot\frac{6}{18}=\frac{93}{18}\).
5.6.2 Satunnaisvektorin kovarianssi ja varianssi
Yksiulotteisen satunnaismuuttujan tilanteessa tarkastellaan usein varianssia satunnaismuuttujan vaihtelun mittana. Moniulotteisen satunnaismuuttujan \(X=(X_1,X_2,...,X_n)\) tilanteessa vastaava koko satunnaisvektorin yhteisvaihtelua kuvaava suure on kovarianssimatriisi, jolle käytetään usein symbolimerkintää \(\Sigma\).
Kovarianssimatriisi \(\Sigma\) koostuu alkioista \[\Sigma_{ij}=Cov(X_i,X_j)=E\left( (X_i-\mu_i)(X_j-\mu_j)\right)=E(X_iX_j)-\mu_i\mu_j\]
Matriisimuotoon kirjoitettuna kovarianssimatriisi on siis \[ \Sigma=\left[ \begin{array}{cccc} E((X_1-\mu_1)(X_1-\mu_1)) & E((X_1-\mu_1)(X_2-\mu_2)) & \cdots & E((X_1-\mu_1)(X_n-\mu_n)) \\ E((X_2-\mu_2)(X_1-\mu_1)) & E((X_2-\mu_2)(X_2-\mu_2)) & \cdots & E((X_2-\mu_2)(X_n-\mu_n)) \\ \vdots & \vdots & \ddots & \vdots\\ E((X_n-\mu_n)(X_1-\mu_1)) & E((X_n-\mu_n)(X_2-\mu_2)) & \cdots & E((X_n-\mu_n)(X_n-\mu_n)) \end{array} \right] \]
5.6.2.1 Kovarianssimatriisin ominaisuuksia:
- Kovarianssimatriisi on symmetrinen.
- Kovarianssimatriisin determinantti on aina ei-negatiivinen (tarkemmin kurssin ulkopuolisin määrittelyin: matriisin tulee olla positiivisesti semidefiniitti).
- Kovarianssimatriisin diagonaalin elementit sisältävät satunnaismuuttujien \(X=(X_1,X_2,...,X_n)\) varianssit, ja tämän takia kovarianssimatriisia kutsutaankin joskus nimellä varianssi-kovarianssimatriisi.
Esimerkki 5.6.2.1
Oletetaan, että satunnaismuuttujien \(X_1\) ja \(X_2\) yhteisjakauma noudattaa (aiemmissa
esimerkeissä käytettyä) yhteisjakaumaa
\[
\begin{array}{c|c|c}
\hline
& X_1=1& X_1=2 \\ \hline
X_2=3 & \frac{3}{18} & \frac{4}{18} \\ \hline
X_2=4 & \frac{5}{18} & \frac{6}{18} \\ \hline
\end{array}.
\]
Laske muuttujien \(X_1\) ja \(X_2\) välinen kovarianssi sekä kovarianssimatriisin muut elementit.
Ratkaisu
Lasketaan aluksi \(Cov(X_1,X_2)\), joka on 2x2-kokoisen
kovarianssimatriisin yhteinen ei-diagonaalialkio. Määritelmän mukaan
\(Cov(X_1,X_2)=E(X_1X_2)-E(X_1)E(X_2)\) ja koska aiemmassa tehtävässä
saatiin \(E(X_1)=\frac{28}{18}\) ja \(E(X_2)=\frac{65}{18}\) riittää
laskea vain suure \(E(X_1X_2)\). Tämä saadaan käyttämällä aiempaa
odotusarvon määritelmää, kun funktio \(g(x,y)=xy\). Tämä saadaan
laskettua diskreetissä tapauksessa painottamalla satunnaismuuttujien
mahdollista tuloa niitä vastaavilla todennäköisyyksillä. Nyt saadaan
siis
\(E(X_1X_2)=3\cdot 1\cdot\frac{3}{18}+3\cdot 2\cdot\frac{4}{18}+4\cdot1\cdot\frac{5}{18}+4\cdot2\cdot\frac{6}{18}=\frac{101}{18}\)
Kysytyksi kovarianssiksi saadaan siis:
\(Cov(X_1,X_2)=E(X_1X_2)-E(X_1)E(X_2)=\frac{101}{18}-\left(\frac{28}{18}\right)\left(\frac{65}{18}\right).\)
Kovarianssimatriisiin kuuluu myös muuttujien varianssit \(Var(X_1)\) ja \(Var(X_2)\).
Aiemman yksiulotteisen varianssin määritelmän mukaan tiedetään, että \(Var(X)=E(X^2)-(E(X))^2\).
Näin ollen käyttäen aiemman tehtävän tuloksia saadaan \(Var(X_1)=E(X_1^2)-(E(X_1))^2=\frac{48}{18}-\left(\frac{28}{18}\right)^2\) ja vastaavasti
\(Var(X_2)=\frac{239}{18}-\left(\frac{65}{18}\right)^2\).
5.7 Ehdolliset jakaumat
Aiemmin yhteisjakaumasta johdettu marginaalijakauma voi olla monissa tilanteissa höydyllinen yksinkertaistus. Toinen vastaava hyödyllinen jakauma usean satunnaismuuttujan tapauksessa on ehdollinen jakama. Tämä haluttujen satunnaismuuttujien jakauman, kun muut satunnaismuuttujat on kiinnitetty tiettyyn arvoon. Nyt esimerkiksi \(f_{X|Y}(x|y)\) kertoo satunnaismuuttujan \(X\) ehdollisen jakauman, kun satunnaismuuttuja \(Y\) on kiinnitetty arvoon \(Y=y\). Ehdollinen jakauma voi olla yksi- tai moniulotteinen. Ehdollisten jakaumien laskemiseen voidaan käyttää aiemmin opittua ehdollisen todennäköisyyden (Bayesin) kaavaa \[P(A|B)=\frac{P(A,B)}{P(B)}\] joka voidaan kirjoittaa myös yleisemmin jakaumille
Ehdollinen jakauma (Bayesin kaava jakaumille): \[f_{X|Y}(x|y)=\frac{f_{X,Y}(x,y)}{f_Y(y)} \] jossa \(f_Y(y)\) on \(Y\):n marginaalijakauma (aka ehdoton jakauma). Tässä
- \(X\) voi olla satunnaisvektori, jolloin ehdollinen jakauma on satunnaisvektorin \(X\) moniulotteinen jakauma
- \(Y\) voi olla satunnaisvektori, jolloin ehto ja kaavan marginaalijakauma em. Bayesin kaavan nimittäjässä on moniulotteinen jakauma.
Esimerkki 5.7.1 (jatkoa aikaisemmalle esimerkille)
Määritä ehdollinen jakauma \(f_{X_1|X_2}(x_1|x_2=2)\) kun yhteisjakauma on
\[ \begin{array}{c|c|c|c|c|c} & X_1=1 & X_1=2 & X_1=3 & X_1=4 & X_5=5 \\ \hline X_2=1 & 3/125 & 4/125 & 5/125 & 6/125 & 5/125 \\ X_2=2 & 5/125 & 6/125 & 6/125 & 3/125 & 7/125 \\ X_2=3 & 2/125 & 1/125 & 8/125 & 8/125 & 6/125 \\ X_2=4 & 2/125 & 3/125 & 6/125 & 4/125 & 7/125 \\ X_2=5 & 3/125 & 4/125 & 6/125 & 7/125 & 8/125 \\ \end{array} \]
Ratkaisu
Aiemmin lasketusta marginaalijakaumasta saadaan \(f_{X_2}(x_2=2)=\frac{27}{125}\).
Nyt kysytty ehdollinen jakauma saadaan jakamalla yhteisjakauma \(f_{X_1,X_2}(x_1,x_2=2)\) [eli yhteisjakaumasta riviä \(X_2=2\) vastaavat alkiot]
luvulla \(f_{X_1}(x_1=2)=\frac{27}{125}\).
Jakauma on näin ollen
\[
\begin{array}{\|c\|c\|c\|c\|c\|} X_1 = 1|X_2=2 & X_1 = 2|X_2=2 & X_1 = 3|X_2=2 & X_1 = 4|X_2=2 & X_1=5|X_2=2
\\ \hline
\frac{5/125}{27/125} &
\frac{6/125}{27/125} &
\frac{6/125}{27/125} &
\frac{3/125}{27/125} &
\frac{7/125}{27/125}
\end{array} \]
Tämä ehdollinen jakauma täyttää selvästi ptnf:n ehdot (positiivisia ja summautuu ykköseen).
Esimerkki 5.7.2
Oletetaan yhteisjakauma
\[ f_{X,Y}(x,y)=\begin{cases} \frac{(1+y)}{196} &, &x=0,1,...,6\text{ ja } y=0,1,...,6 \\
0 &, &\text{muuten}. \end{cases} \]
Määritä jakauma \(f_{Y|Z}(y|x)\)
Ratkaisu
Kyseessä on diskreetti satunnaismuuttuja, jonka marginaalijakauma
\(f_{X}(x)= \sum_{y=0}^{6} \frac{(1+y)}{196} =\frac{1}{196} \sum_{y=0}^6(1+y)= \frac{1}{196}\left(7+\sum_{y=0}^6y\right)=\frac{1}{196}(7+21)= \frac{1}{7}\), kun \(0 \leq x \leq 6\).
Ehdollinen jakauma on näin ollen \(f_{Y|X}(y|x)=\frac{f_{X,Y}(x,y)}{f_X(x)}=
\frac{7(1+y)}{196}=\frac{(1+y)}{28}\) muuttujien alueella \(x=0,1,...,6\) ja \(y=0,1,...,6\).
Itsenäisenä harjoitustehtävänä voit tarkistaa tämän jakauman matemaattiset ehdot.
Esimerkki 5.7.3 (jatkoa aiemmalle esimerkille)
Jos yhteistiheys on \(f_{X,}(x,y)=e^{-y},
\text{ kun } 0<x<y<\infty\), ja nolla muutoin, niin mikä on jakauma
\(f_{X|Y}(x|y)\)?
Ratkaisu
Aiemmin on laskettu marginaalijakauma \(f_X(x)=e^{-x}, \text { kun }
x <y\) ja \(0\) muulloin. Soveltamalla ehdollisen todennäköisyyden
määritelmää kaavaa saadaan
\(f_{Y|X}(y|x)=\frac{f_{X,Y}(x,y)}{f_X(x)}=\frac{e^{-y}}{e^{-x}}=e^{-(y-x)}\),
kun \(x<y\) ja \(f_{Y|X}(y|x)=\frac{0}{e^{-x}}=0\), kun \(x \geq y\).
5.7.1 Ehdollisen jakauman tunnusluvut
Ehdollisesta jakaumasta voidaan laskea tunnuslukuja aiemmin opituilla tiedoilla - ehdollinen jakauma on aivan tavallinen jakauma. Tyypillisiä kiinnostavia suureita ehdollisesta jakaumasta on ehdollinen odotusarvo ja (ko)varianssi, jotka lasketaan vastaavalla tavalla kuin tavallinen odotusarvo, mutta painottavana tekijänä on nyt ehdollinen jakauma ehdottoman jakauman sijasta.
Ehdollisen jakauman odotusarvo \[E(X|Y=y)=\sum_x x f_{X|Y}(x|y) \text{ (diskreetti tapaus) }\] \[E(X|Y=y)=\int x f_{X|Y}(x|y)dx \text{ (jatkuva tapaus) }\]
Esimerkki 5.7.1.1
Oletaan yhteistiheysfunktio on \(f_{X,Y}(x,y) = \frac{x}{75}\), kun \(0 \leq
X \leq 5\) ja \(0 \leq Y \leq 6\), ja nolla muutoin. Laske \(E(X|Y)\)
Ratkaisu
Lasketaan aluksi
\(f_Y(y)=\int_0^5\frac{x}{75}dx=\frac{1}{6}\). Ehdollinen jakauma
\(f_{X|Y}(x|y)\) on nyt
\(f_{X|Y}(x|y)=f_{X,Y}(x,y)/f_Y(y)=\frac{6x}{75}\). Odotusarvo
\(E(X|Y)\) saadaan nyt integraalista \(\int_{-\infty}^{\infty}x
f_{X|Y}(x|y)dx\), joka tässä tapauksessa saa muodon \(\int_0^5x
\frac{6x}{75}dx=\int_0^5\frac{6x^2}{75}dx=
\frac{6}{75}(\frac{5^3}{3}-\frac{0^3}{3})=\frac{6*125}{75*3}=\frac{10}{3}\).
Huomaa: tässä esimerkissä ehdollinen jakauma
\(f_{X|Y}(x|y)\) ei sisältänyt ollenkaan termiä \(y\), joten on
selvää, että kysytty odotusarvo ei riipu ehdosta eli \(Y\):stä.
Esimerkki 5.7.1.2
Varastossa
on kolmen eri valmistajan tuottamia tuotteita kolmesta eri laatuluokasta
(halpa, normaali ja kallis) ja näiden hinnat sekä suhteelliset osuudet (todennäköisyydet).
\[
\begin{array}{c|c|c|c}
\hline
\hline
Valmistaja & Halpa & Normaali & Kallis \\
\hline
A & 125 & 250 & 900 \\
B & 135 & 350 & 850 \\
C & 85 & 240 & 600 \\
\end{array}.
\]
\[
\begin{array}{c|c|c|c}
\hline
\hline
Valmistaja & Halpa & Normaali & Kallis \\
\hline
A & 1/9 & 2/18 & 3/18 \\
B & 1/18 & 3/18 & 2/9 \\
C & 1/18 & 1/18 & 1/18 \\
\end{array}.
\]
Laske ehdollinen odotusarvo valmistajan B tuotteen hinnalle.
Ratkaisu
Merkitään, että \(X\)=valmistaja ja \(Y\)=laatuluokka.
Selvitetään aluksi ehdollinen jakauma
\(f_{Y|X}(y|x)=f_{XY}(x,y)/f_{X}(x)\), jonka laskemista varten
tarvitaan marginaalijakauma \(f_{X}(x)\). Tämä marginaalijakauma
saadaan laskemalla rivisummat yo. taulukosta ja \(f_{X}(x)\) on siten
\((7/18, 8/18, 3/18)\). Ehdollinen jakauma \(f_{Y|X}(y|x=B)\) saadaan
nyt jakamalla yhteisjakauman todennäköisyydet \(f_{XY}(y,x=B)=(1/18,
3/18, 2/9)\) ehdon todennäköisyydellä eli luvulla \(f_{X}(x=B)=8/18\).
Ehdollinen jakauma \(f_{Y|X}(y\|x=B)\) koostuu nyt todennäköisyyksistä
\((1/8, 3/8, 4/8)\), joka on myös selvästi jakauma koska ovat
ei-negatiivisia ja joiden summa on 1.
Ehdollinen odotusarvo valmistajan B tuotteen hinnalle saadaan nyt painottamalla tulosvaihtoehtoja eli valmistajan B keskihintoja (135, 350 ja 850) näitä vastaavilla todennäköisyyksillä, jotka saadaan edellä lasketusta ehdollisesta jakaumasta. Ehdolliseksi odotusarvoksi saadaan siis: \(135*1/8+350*3/8+850*4/8=573.123\).
5.7.2 Regressiofunktio
Kun kahden satunnaismuuttujan \(X,Y\) tapauksessa tarkastellaan ehdollista odotusarvoa \(E(X|Y=y)\) muuttujan \(y\) funktiona, niin tätä funktiota kutsutaan \(X\):n regressiofunktioksi \(Y\):n suhteen. Samojen satunnaismuuttujien tilanteessa funktio \(E(Y|X=x)\) on \(Y\):n regressiofunktio \(X\):n suhteen. Regressiofunktio kertoo siis kohdemuuttujan odotusarvon riippuvuuden ehtomuuttujan suhteen. Koska \(X\) on satunnaismuuttuja, niin regressiofunktio ei tietystikään kerro tarkkaan ottaen mikä on \(X\) arvo tietyllä \(y\):n arvolla vaan se kertoo ainoastaan odotusarvon.
Esimerkki 5.7.2.1 (jatkoa esimerkille 5.7.3)
Määritä regressiofunktio \(x\):n suhteen, kun
\(f_{X,Y}(x,y)=e^{-y}, \text{ kun } 0 <x <y<\infty\).
Ratkaisu
Regressiofunktion määritelmästä saadaan
regressiofunktioksi \(E(Y|X=x)=\int_x^{\infty} ye^{-(y-x)}dy\).
Käyttämällä hieman edistyksellisempiä integrointitaitoja
(osittaisintegrointia) tai jotain ulkoista integraattoria (esim.
tätä)
saadaan tästä integroinnista tulokseksi \(E(Y|X=x)=1+x\), joka on siis
lineaarinen suora kulmakertoimella 1 ja vakiotermillä 1.
5.8 Lisätietoa: moniulotteiset marginaalijakaumat ja ehdolliset odotusarvot
Tyypillisesti tarkasteltavat marginaalijakaumat ovat yksiulotteisia, mutta joissakin tilanteissa on tarvetta moniulotteisille marginaalijakaumille. Esimerkiksi neliulotteisesta diskreetistä yhteisjakaumasta \(f_{X,Y,Z,G}(x,y,z,g)=P(X=x, Y=y, Z=z,G=g)\) voidaan laskea seuraavat kaksiulotteiset diskreetit marginaalijakaumat \[f_{X,Y}(x,y)=\sum_{z}\sum_{g}f_{X,Y,Z,G}(x,y,z,g)\] \[f_{X,Z}(x,z)=\sum_{y}\sum_{g}f_{X,Y,Z,G}(x,y,z,g)\] \[f_{X,G}(x,g)=\sum_{y}\sum_{z}f_{X,Y,Z,G}(x,y,z,g)\] \[f_{Y,Z}(y,z)=\sum_{x}\sum_{g}f_{X,Y,Z,G}(x,y,z,g)\] \[f_{Y,G}(y,g)=\sum_{x}\sum_{z}f_{X,Y,Z,G}(x,y,z,g)\] \[f_{Z,G}(z,g)=\sum_{x}\sum_{y}f_{X,Y,Z,G}(x,y,z,g)\]
Vastaavasti voitaisiin laskea neliulotteisen jatkuvan tiheysfunktion \(f_{X,Y,Z,G}(x,y,z,g)\) kaksiulotteiset marginaalijakaumat analogisesti edellisen tapauksen kanssa vaihtamalla summaus integrointiin.
Moniulotteiset ehdolliset odotusarvot voidaan laskea vastaavalla tavalla kuin aiemmin yksiulotteiset ehdolliset odotusarvot: painottamalla satunnaisvektorin tulosvaihtoehtoja näitä vastaavalla moniulotteisella ehdollisella jakaumalla. Esimerkiksi \(E(X,Z,W|Y=y)\) saadaan painottamalla \((X,Z,W)\) tulosvaihtoehtoja jakaumalla \(f_{X,Z,W|Y}(x,z,w|Y=y)\).
