7 Lineaarinen regressio
Aiemmilla taustatietokursseilla on tehty selitettävälle muuttujalle erilaisia yhden selittävän muuttujan regressiomalleja. Tässä kappaleessa tarkastellaan lineaarista mallia, jossa on useampi kuin yksi selittävä muuttuja. Tämä on mallinnuskehikkona huomattavasti käytännöllisempi useimpiin tosielämän tilanteisiin ja ilmiöihin, jotka ovat usein moniulotteisia. Tässä kappaleessa tuodaan myös eksplisiittisesti näkyväksi regressiomalleissa implisiittisesti tehtyjä taustaoletuksia, joiden voimassaoloa on joskus syytä kriittisesti tarkastella vastaavalla tavalla kuin hypoteesin testauksessa.
Lineaarinen regressio ja laajemmin regressioanalyysi voidaan nähdä jatkumona aiemmalle hypoteesintestaukselle, jossa on koitettu vastata tilastollisen hypoteesintestauksen keinoin mm. kysymykseen “onko eroa” tai “onko vaikutusta”. Regressioanalyysin lopputuloksena voidaan vastata mm. kysymyksiin, “kuinka paljon on vaikutusta” tai “mikä on efektin suuruus”. Näihin vastauksiin perustuen voidaan tehdä edelleen ennustusta, esimerkiksi tuotannonsuunnittelua, kun tunnetaan efektien suuruus ja merkitsevyys.
7.1 Yhden selittäjän lineaarisen mallin kertaus
Tavallisessa yksiulotteisessa lineaarisessa regressiossa tehdään selitettävälle muuttujalle \(y\) muotoa \(y=ax+b\) oleva lineaarinen selitysmalli perustuen kerättyihin kiinteisiin ja kaksiulotteisiin havaintopareihin \((y_i,x_i)\), \(i=1,\ldots ,n\), jossa yksiulotteiset \(x_i\):t ovat selittäviä muuttujia ja \(y_i\):t ovat selitettäviä muuttujia. Yksittäiselle havaintoparille \((y_i, x_i)\) on voimassa selitysmalli \[y_i = \hat{a}x_i +\hat{b} + \epsilon_i.\] Tässä \(\epsilon_i =y_i-(\hat{a}x_i +\hat{b})\) on havaintopariin \((y_i, x_i)\) liittyvä erotus havainnon \(y_i\) ja lineaarisen mallin antaman teoreettisen ennusteen eli ns. systemaattisesta osan \(\hat{a}x_i +\hat{b}\) välillä. Suure \(\epsilon_i\) voi olla positiivinen, negatiivinen tai nolla. Suureita \(\epsilon_i\) kutsutaan usein myös residuaaleiksi tai ‘virheiksi’ ja joskus myös ‘poikkeamiksi’. Tämä viimeinen termi on kuitenkin siinä mielessä huono, että matematiikassa poikkeama määritellään itseisarvona, eikä näin ollen voi saada negatiivisia arvoja.
7.1.1 Taustaoletukset yhden selittäjän lineaarisessa regressiossa
Yhden selittävän muuttujan lineaarisessa regressiossa yksittäisille residuaaleille \(\epsilon_i\) tehdään lähes poikkeuksetta - joskin hyvin usein implisiittisesti - seuraavat perusoletukset
- Residuaalit \(\epsilon_i\) ovat keskenään samoin jakautuneita
- Residuaaleille pätee \(E(\epsilon_i)=0\) eli keskimäärin poikkeamat ovat nolla
- Residuaalit eivät riipu selittävän muuttujan \(x\) arvoista vaan ovat tästä riippumattomia. (Huom: riippuvuus tässä kohdin tarkoittaisi esimerkiksi sitä, että residuaalit kasvaisivat tai pienenisivät systemaattisesti selittävän muuttujan arvojen muuttuessa)
- Residuaalit ovat keskenään riippumattomia eli yhden erotuksen arvo ei vaikuta toisen erotuksen arvoon
- Homoskedastisuusehto: residuaaleilla on keskenään samat varianssit eli \(Var(\epsilon_i)=\sigma^2=\)vakio
- Selittävät muuttujat \(x_i\) ovat kiinteitä ja niiden havainnot on toisistaan lineaarisesti riippumattomia
Tämä taustaoletusten lista formuloidaan joskus hieman eri tavalla sisällön pysyessä oleellisesti samana ja joskus osa näistä oletuksista jätetään pois (tai jätetään mainitsematta). Joissain harvinaisissa tilanteissa näitä taustaehtoja formuloidaan myös lisää.
7.1.2 Pienimmän neliösumman menetelmä
Muotoa \(y=ax+b\) oleva lineaarisen mallin sovitus eli optimaalisten regressioparametrien \(\hat{a}\) ja \(\hat{b}\) hakeminen tehdään useimmiten minimoimalla poikkeamien neliösummaa, jolloin optimointitehtävä on \[min \sum_{i=1}^{n} \epsilon_{i}^{2}.\] Tämä neliösumman minimointi on tässä vaiheessa puhtaan matemaattinen kriteeri, eikä perustu mihinkään tiettyyn jakaumaoletukseen (esim. normaalijakaumaan). Tätä minimointikriteeriä kutsutaan yleisesti pienimmän neliösumman menetelmäksi (PNS) (En: Least squares).
Edellä mainituilla taustaoletuksilla poikkeamille ja käyttäen PNS-kriteeriä voidaan optimaalisille regressioparametreille yhden selittäjän lineaarisessa mallissa johtaa seuraavat kaavat \[\hat{a} = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n}(x_i - \bar{x})^2} = \frac{Cov(x,y)}{Var(x)}\] \[\hat{b} = \bar{y} - \hat{a}\bar{x}.\] Yksityiskohtiin perehtyminen näiden tulosten johtamisessa jätetään oman harrastuksen varaan.
Lineaarisen suoran parametrien sovittamiseen on olemassa muitakin matemaattisia kriteerejä kuin PNS. Yksi tällainen on poikkeamien itseisarvosumman minimointi \(min \sum_{i}|\epsilon_i|\), jolla on tiettyjä hyviä teoreettisia ominaisuuksia verrattuna PNS-menetelmään, joka on suhteellisen herkkä esimerkiksi poikkeavien havaintojen suhteen (ns. robustisuus aspekti). Nämä muut minimointikriteerit ovat kuitenkin vähemmän käytettyjä, sillä niiden teoria ja käytäntö ovat PNS-menetelmää hankalampia.
PNS-menetelmää voidaan käyttää vastaavalla tavalla kriteerinä etsimään minkä tahansa muun regressiomallin, esimerkiksi neliöllisen mallin parametrejä. Minimoitavana kriteerinä on tällöin aivan vastaavasti residuaalien neliösumma, jossa residuaalit määritellään erotuksina havaintojen ja ennusteiden välillä
7.2 Useamman selittävän muuttujan lineaarinen regressio
Monen selittävän muuttujan regressiossa yksiulotteisen selitettävän muuttujan \(y\) selittäjänä eli kovariaattina on yksiulotteisen \(x\):n sijasta \(k\)-ulotteinen vektori \(x=[x_1, x_2,\ldots,x_k]^T\).Monen selittävän muuttujan lineaarisessa regressiossa selitysmalli yksiulotteiselle \(y\):lle on muotoa \[y= b_{0} + b_{1}x_{1} + b_{2}x_{2} \ldots + b_{k}x_{k},\] jossa \(b_0\) on vakiotermi ja termi \(b_l\) on selittävää muuttujaa \(x_l\) vastaava kerroin, joka kertoo selitettävän muuttujan muutoksesta \(x_l\):n suhteen.
7.2.1 Parametrien ratkaisu monen selittäjän regressiossa
Monen muuttujan lineaarinen regressio perustuu yksiulotteisen lineaarisen regression tavoin havaintopareihin \((y_i,x_i)\), \(i=1,\ldots,n\), jossa selittävä havainto on nyt havaintovektori \(x_i=[x_{i1},x_{i2},\ldots,x_{ik}]^T\). Yksittäiselle havaintopisteelle selitysmalli on muotoa \[y_i= b_{0} + b_{1}x_{i1} + b_{2}x_{i2} + \ldots + b_{k}x_{ik} + \epsilon_i,\] jossa \(\epsilon_i\) on vastaava yksiulotteinen residuaalitermi kuin aiemmin.
Selitysmalli voidaan kirjoittaa myös kompaktiin matriisimuotoon \[y = Xb + \epsilon,\] jossa
- vektori \(y = [y_1,y_2, \ldots, y_n]^T\) on kokoa \(n\) oleva vektori selitettävän muuttujan havainnoista,
- vektori \(\epsilon = [\epsilon_1,\epsilon_2, \ldots, \epsilon_n]^T\) on kokoa \(n\) oleva vektori sisältäen residuaalit \(\epsilon_i\)
- vektori \(b = [b_0,b_1, \ldots, b_k]^T\) on kokoa \(k+1\) oleva (pysty)vektori koostuen vakiotermistä \(b_0\) ja kertoimista \(b_1,\ldots,b_k\)
- matriisi \(X\) on muotoa
\[X = \left[ \begin{array}{cccc}
1&x_{11} &\cdots &x_{1k}\\
\vdots & \vdots& \ddots& \vdots \\
1&x_{n1}&\cdots& x_{nk}
\end{array} \right] \]
ja tätä selittävät muuttujat sisältämää matriisia kutsutaan yleisesti ns. design-matriisiksi. Tämän matriisin ensimmäinen sarake on vektori ykkösiä, joka vastaa matriisikertolaskussa termiä \(1\cdot b_0\).
Käytössä ajatellaan olevan \(n\) kappaletta riippumattomia havaintoja \((y_i, x_i)\), ja jossa minimivaatimus on,
että \(n \geq k\) eli havaintoja pitää olla vähintään yhtä paljon kuin regressiomallissa on
selittäjiä. Mikäli näin ei ole, niin parametrejä ei ole mahdollista estimoida ollenkaan. Usein
toivotaan lisäksi, että \(n \gg k\) eli havaintoja on paljon enemmän kuin selittäviä muuttujia.
7.2.2 Taustaoletukset ja parametrien ratkaisu
Monen selittävän muuttujan regression yhteydessä taustalle tehdään tyypillisesti samat oletukset residuaaleille \(\epsilon_i\) kuin yksiulotteisessa tapauksessa. Näiden lisäksi oletetaan, että suureet \(x_{is}\) ovat lineaarisesti riippumattomia suureista \(x_{ih}\) (\(s\neq h\)) kaikilla havainnoilla \(i\) eli selittävät tekijät eivät riipu toisistaan. Näistä oletuksista seuraa, että \[E(y_i)=b_{0} + b_{1}x_{i1} + b_{2}x_{i2} + \ldots + b_{k}x_{ik}\] ja \[Var(y_i)=\sigma^2.\]
Parametrien standardiratkaisu monen selittäjän tapauksessa perustuu poikkeamien neliösumman minimointiin vastaavalla tavalla kuin yhden selittäjän tapauksessa ja optimointitehtävä on siis
\[min \sum_{i=1}^n \epsilon_i^2= min \sum_{i=1}^n \left(y_i-x_ib\right)^2,\]
jossa \(x_i\) on design-matriisin \(X\) rivi \(i\), jonka ensimmäinen komponentti on 1 vastaten kerroinvektorin \(b\) vakiotermiä \(b_0\).
Ilman teoreettisia perusteluja todetaan, että tämän optimointitehtävän ratkaisu saadaan ns. normaaliyhtälön (EN: normal equation) \[X^TX\hat{b}=X^Ty\] ratkaisuna \(\hat{b}\):n suhteen, joka on \[\hat{b}=(X^TX)^{-1}X^Ty.\] Tässä vektorin \(\hat{b}\) ensimmäinen elementti on vakiotermi \(\hat{b}_0\) ja seuraavat elementit \(\hat{b}_1,...,\hat{b}_k\) ovat muuttujakohtaisia kertoimia eli ns. efektikertoimia tai efektejä.
7.2.3 Ratkaisun olemassaolo ja multikollinearisuus
Edellä kuvattu ratkaisu regressioparametreille on matemaattisesti mahdollinen vain jos matriisi \(X^TX\) on kääntyvä eli sillä on olemassa käänteismatriisi. Matriisin \(X^TX\) käänteismatriisin olemassaolo perustuu selittävien muuttujien riippumattomuuteen - mikäli kaikki selittävät muuttujat ovat keskenään lineaarisesti riippumattomia (“erillisiä”), niin matriisi on kääntyvä. Mikäli jotkut selittävät muuttujat ovat keskenään täydellisesti lineaarisesti riippuvia ei matriisi \(X^TX\) ole kääntyvä. Mikäli jotkut muuttujat ovat paljon - muttei täydellisesti - keskenään lineaarisesti riippuvia, niin matriisi \(X^TX\) on periaatteessa kääntyvä, jolloin ratkaisu \(\hat{b}\) voidaan laskea, muttaratkaisu on ns. numeerisesti epästabiili. Tällöin mm. hyvinkin pienet muutokset selittävän muuttujan arvoissa voivat vaikuttaa radikaalisti ratkaisuun tai ratkaisun laskeminen on numeerisesti muutoin hankalaa.
Ilmiötä, jossa jotkut selittävät muuttujat ovat keskenään lineaarisesti riippuvia kutsutaan multikollineaarisuudeksi. Tämän ilmiön suuruutta ja samalla matriisin \(X^TX\) kääntyvyyttä voidaan tarkastella monilla tämän kurssin ulkopuolisilla matemaattisemmilla menetelmillä tai yksinkertaisesti esimerkiksi tutkimalla aineiston korrelaatiomatriisia, joka saadaan standardoimalla kovarianssimatriisin elementit muuttujien keskihajonnoilla. Korrelaatiomatriisi on siis \[ \left[\begin{array}{ccc} \frac{Cov(x_1,x_1)}{s(x_1)s(x_1)}&\cdots&\frac{Cov(x_1,x_k)}{s(x_1)s(x_k)}\\ \vdots&\ddots&\vdots\\ \frac{Cov(x_k,x_1)}{s(x_k)s(x_1)}&\cdots&\frac{Cov(x_k,x_k)}{s(x_k)s(x_k)} \end{array} \right], \] jossa \(Cov(x_j,x_m) = \frac{1}{n-1}\sum_{i=1}^{n}(x_{ij}-\bar{x}_j)(x_{im}-\bar{x}_m)\) on otoskovarianssi \(x_j\):n ja \(x_m\):n välillä, ja \(s(x_j)=\frac{1}{n-1}\sum_{i=1}^{n}(x_{ij}-\bar{x}_j)^2\) on muuttujan \(x_j\) otosvarianssi.
Tästä matriisista nähdään helposti muuttujat, jotka ovat keskenään voimakkaasti lineaarisesti riippuvia eli joilla otoskorrelaation itseisarvo on lähellä arvoa yksi. Tähän korrelaatiomatriisiin perustuen on mahdollista sisällyttää malliin vain sellaiset muuttujat, joiden välillä lineaariset riippuvuudet ovat riittävän pieniä eli muuttujat ovat riittävän “erillisiä”. Tarkkaa standardisääntöä ei kuitenkaan ole olemassa minkä suuruiset korrelaatiot selittävien muuttujien välillä on vielä hyväksyttäviä ja mitkä ei. Selittävien muuttujien valintaa tukemaan on kuitenkin olemassa erilaisia mallinvalintaproseduureja, joita tarkastellaan seuraavassa.
7.3 Mallin valinnan ja sovituksen tarkasteluja
Lineaarisen mallin sovitus on teknisesti periaatteessa usein hyvin suoraviivaista ja yksinkertaista, ja tarjoaa joskus - ainakin näennäisesti - hyvinkin uskottavan näköisen kuvauksen selitettävästä ilmiöstä. Tästä huolimatta lineaariseen mallinnukseen tai yleisemmin regressiofunktion sovitukseen kannattaa suhtautua kriittisesti ja huolellisesti, sillä esimerkiksi mahdollisia lineaarisia selitysmalleja voi olla useita eikä paraskaan valituista selitysmalleista välttämättä toteuta oletettuja lineaarisen mallin taustaehtoja tai muutoin sovi kuvaamaan annettua aineistoa tai ilmiötä. Ilman huolellista pohdintaa ja kriittistä tarkastelua tehty mallinsovitus - oli se sitten yksinkertainen lineaarinen malli tai monen muuttujan eksoottinen malli - on yksinkertaisesti huonoa tilastotiedettä.
7.3.1 Selittävien muuttujien valinnasta monen selittäjän regressiossa
Mallin selittäviksi muuttujiksi voidaan periaatteessa valita mitä tahansa mahdollisia “riittävän erillisiä” muuttujia, joista on riittävästi täydellisiä havaintoja eli kaikille selittäville muuttujille tulee olla sama määrä havaintoja kuin selitettäville muuttujille - tästä tosin voidaan kurssin ulkopuolisissa edistyneemmissä ja vaativammissa tarkasteluissa tietyin ehdoin varovasti luopua. Aloittelijan tyyppivirhe selittävien muuttujien valinnassa on käyttää aina kaikkia mahdollisia muuttujia selittämään ilmiötä ilman systemaattista ja kriittistä mallinvalintatarkastelua, johon kuuluu sekä kvantitatiivinen mallinvalintatarkastelu että (semi)laadulliset periaatteet. Jälkimmäiseen kategoriaan kuuluu mm. seuraavat perusperiaatteet
Kausaalisuus: selittäjän tulee uskottavasti vaikuttaa selitettävään – mieluusti suoraan, mutta joskus mahdollisesti myös välillisesti. Yleensä pyritään välttämään myös takaisinkytkentämahdollisuutta eli tilannetta, jossa selittävä muuttuja vaikuttaa selitettävään, joka edelleen vaikuttaa takaisin selitettävään muuttujaan. Kausaalisuuden pohdintaan tarvitaan lähes aina jotain substanssitietoa - joko itse tai muualta hankkien. Kausaalisuuden kvantitatiiviseen tutkimiseen on olemassa myös edistyneempiä menetelmiä, mutta ne jätetään tämän kurssin ulkopuolelle.
Paljon ei (automaattisesti) ole parempi: hyvin monen selittäjän malli voi olla selityskyvyltään hyvä mutta ennustekyvyltään huono ja varsin usein yksinkertaisempi malli vähemmillä selittäjillä voi usein olla aivan riittävä. Muuttujien määrän valinnassa voi käytännössä painaa myös se, että hyvin monen muuttujan käyttö esimerkiksi myöhemmässä ennustamisessa voi olla haastavaa sen takia, että joidenkin muuttujien hankinta voi olla esimerkiksi kallista tai muuten hankalaa. Ks. myös (ks. Occam’s razor, KISS)
Nämä perusperiaatteet yhdessä osin alla esiteltävien kvantitatiivisten kriteerien kanssa toimivat sekä selittävien muuttujien valintaan että laajemminkin mallinvalintaan.
7.3.2 Kriteerejä kvantitatiiviseen mallinvalintaan
7.3.2.1 Selitysaste
Klassinen ja aiemmilla taustatietokursseilla käytetty mittari mallin valinnan hyvyyteen on selitysaste \(R^2\), joka yleisesti määritellään osamääränä \[ R^2 = \frac{SSR}{SST}\] jossa
- \(SST=\sum_{i=1}^{n}(y_i - \bar{y})^2\) (Sum of Squares Total) kertoo yksittäisen selitettävien havaintojen neliöpoikkeamasta suhteessa selitettävien havaintojen keskiarvoon
- \(SSR= \sum_{i=1}^{n}(\hat{y}_i - \bar{y})^2\) (Sum of Squares Regression) kertoo mallin mukaisten selitettävien muuttujien estimaattien neliöpoikkeamasta suhteessa selitettävien havaintojen keskiarvoon
- \(SSE=\sum_{i=1}^{n}(y_i-\hat{y}_i)^{2}=\sum_{i=1}^{n}\epsilon_{i}^{2}\) (Sum of Squares Error) kertoo yksittäisten selitettävien havaintojen neliöpoikkeamasta suhteessa mallin mukaisten selitettävien muuttujien estimaatteihin.
Näillä merkinnöillä on voimassa ns. neliösummahajotelma \(SST=SSR+SSE\). Tätä hajotelmaa käyttäen voidaan mallin selitysaste kirjoittaa muodossa \[ R^2 = \frac{SSR}{SST} = 1- \frac{SSE}{SST}\]. Yhden selittäjän lineaarisen mallin tapauksessa tämä redusoituu muotoon \(R^2=r^2\), jossa \(r\) on otoskorrelaatiokerroin selitettävän ja selittävän muuttujan välillä.
Selitysaste \(R^2\) kuvaa kuinka hyvin kuinka paljon \(y\):n vaihtelusta selittyy \(x\):n vaihtelulla tarkasteltavan regressiomallin kautta ja siten toimii yhtenä mittarina kuinka mallin tuottamat estimaatit sopivat havaintoihin.
7.3.2.2 Adjustoitu selitysaste \(R_{adj}^2\)
Edellä kuvatun selitysasteen ܴ\(R^2\) ominaisuus on, että lisättäessä selittäviä muuttujia malliin selitysaste paranee (tai pysyy vähintään samana) vaikkei selittäjillä olisikaan mitään oleellista merkitystä mallin selityksessä. Selittävien muuttujien lisäämisen kohdalla on myös huomattava, että mallin parametriestimoinnin “estimointikustannus” nousee jokaisen lisättävän selittävän muuttujan myötä ja esimerkiksi havaintoja tarvitaan enemmän mallissa, jossa selittäviä muuttujia on enemmän. Näiden seikkojen takia on johdettu ns. adjustoitu selitysaste \(R^2_{adj}\), joka määritellään \[R^2_{adj} = 1 - (1- R^2 )\left(\frac{n-1}{n-k-1}\right).\] Tämä suure ottaa eksplisiittisesti huomioon selittäjien lukumäärän (\(k\)) sekä havaintojen lukumäärän (\(n\)) ja “rankaisee” suuresta määrästä selittäviä muuttujia.
7.3.2.3 Muita kriteerejä
Edellä mainittujen yksinkertaisten kriteerien lisäksi mallinvalintaan on olemassa paljon muitakin kilpailevia tapoja, jotka kaikki pyrkivät omalla tavallaan kertomaan mallin hyvyydestä ja tarjoamaan tietyssä mielessä parhaan mallin. Useimmat näistä vaativat kuitenkin paljon enemmän matemaattista pohjustusta kuin tämän kurssin puitteissa on mahdollista käydä läpi ja näihin perehtyminen jätetään oman harrastuksen varaan (ks. esim. sivu).
Huomattavaa on kuitenkin se, että joskus eri kriteerit tarjoavat samanlaisia mallirakenteita ja joskus nämä eroavat toisistaan merkittävästikin. Vaikka jokainen mallinvalinnan kriteeri onkin yksittäin ei-subjektiivinen, niin kriteerin valinta on loppujen lopuksi ei-triviaalia. Mallinvalintaa onkin joskus kutsuttu tieteeseen perustuvaksi taiteeksi. Tämä lause pitää sisällään myös sen seikan, että kaikkia subjektiivisiakin valintoja pitää kuitenkin pystyä uskottavasti perustelemaan.
7.3.3 Proseduureja selittävien muuttujien valintaan
Yksi paljon käytetty tapa muuttujien valintaan on käyttää portaittaista proseduuria: lisätään muuttujia yksi kerrallaan pieneen määrään alkumuuttujia, kunnes valittu mallinvalintakriteeri saavuttaa huippukohtansa (ns. forward selection). Saman voi toki toteuttaa myös vähentämällä muuttujia yksi kerrallaan suuresta määrästä alkumuuttujia (ns. backward selection). Portaittaisessa proseduurissa pitää myös jollakin tavalla määrittää lisättävien (tai poistettavien) muuttujien järjestys.
Joissakin ohjelmistoissa on valmiina tällainen portaittainen mallinvalinta joko täysautomaattisena tai semiautomaattisena. Vaikka tällainen mallinvalinnan ulkoistaminen saattaakin tuntua houkuttelevalta, niin näihin automaattisiin ohjelmistojen antamiin päätöksiin tulee suhtautua kuitenkin kriittisesti ja tilastotieteen näkökulmasta tulisi minimissään tuntea perusteet, joilla valinta on tehty.
Toinen joskus käytetty tapa muuttujien valintaan on käyttää ns. konsensusperiaatetta. Tässä mallinvalinta tehdään useita kriteerejä käyttäen ja lopulliseksi malliksi valitaan se, mikä sai eniten tukea eri mallikriteereiltä. Tasapelitilanteessa päätös tehdään jollakin sopivalla heuristiikalla.
7.3.4 Tämän kurssin proseduuri selittävien muuttujien valintaan
Jotta käytännön mallinvalinta ei kuitenkaan jäisi edellä kuvatun valinnanvaikeuden jälkeen aivan liian ambivalentiksi, niin seuraavassa on listattu yksinkertainen polku lineaarisen regression muuttujien valintaan, jota käytetään tämän kurssin harjoituksissa.
- Lasketaan korrelaatiot selittävien ja selitettävän muuttujan välillä ja listataan muuttujat laskevaan järjestykseen sen mukaan kuinka suuri korrelaatiokerroin tällä on selitettävän muuttujan kanssa
- Valitaan suurimman korrelaation sisältävä muuttuja ja määritetään mallin hyvyys käyttäen suuretta \(R^2_{adj}\)
- Lisätään malliin selittäviä muuttujia kohdan 1 listan mukaan, kunnes on saavutettu optimi
Tällä proseduurilla päästään ainakin suboptimaaliseen ratkaisuun kyseisen kriteerin suhteen. Tässä on kuitenkin huomattava, että selittävien muuttujien lisäykset tehdään tässä perustuen yksittäisten muuttujien korrelaatioihin selitettävän muuttujan kanssa ja optimaalinen ratkaisu voi olla tämän proseduurin ulottumattomissa.
7.3.5 Residuaalien tutkiminen osana mallinsovitusta
Edellä kuvatun mallinvalinnan ohella mallinsovitukseen kuuluu oleellisena osana myös ns. residuaalianalyysi. Tässä tavoitteena on tutkia jälkikäteisesti residuaaleja koskevien taustaoletuksien voimassaoloa alustavasti valitulla regressiomallilla. Aiemmin listattujen taustaoletusten mukaisesti residuaalit eivät esimerkiksi riipu selittävän muuttujan arvosta ja ovat keskenään riippumattomia. Tätä voidaan visuaalisesti tutkia esimerkiksi hajontakuviosta, johon on piirretty residuaalit ja näitä vastaavat selittävän muuttujan arvot. Myös tilanne, jossa residuaalit systemaattisesti ovat suurempia tai pienempiä selittävän muuttujan kasvaessa on mahdollista havaita pistekuviosta.
Esimerkki 7.3.4.1
Esimerkkinä residuaalianalyysista oheinen kuvapari, jossa a-kuvasta havaitaan peräkkäisten residuaalien olevan tyypillisesti samanmerkkisiä eli käyttäytyvän syklisesti. Vastaavasti b-kuvasta nähdään selkeästi residuaalisen itseisarvojen riippuvuus selittävän muuttujan arvoista. Kumpikin näistä residuaaliploteista on ristiriidassa lineaarisen mallin yleisten residuaalioletusten kanssa.
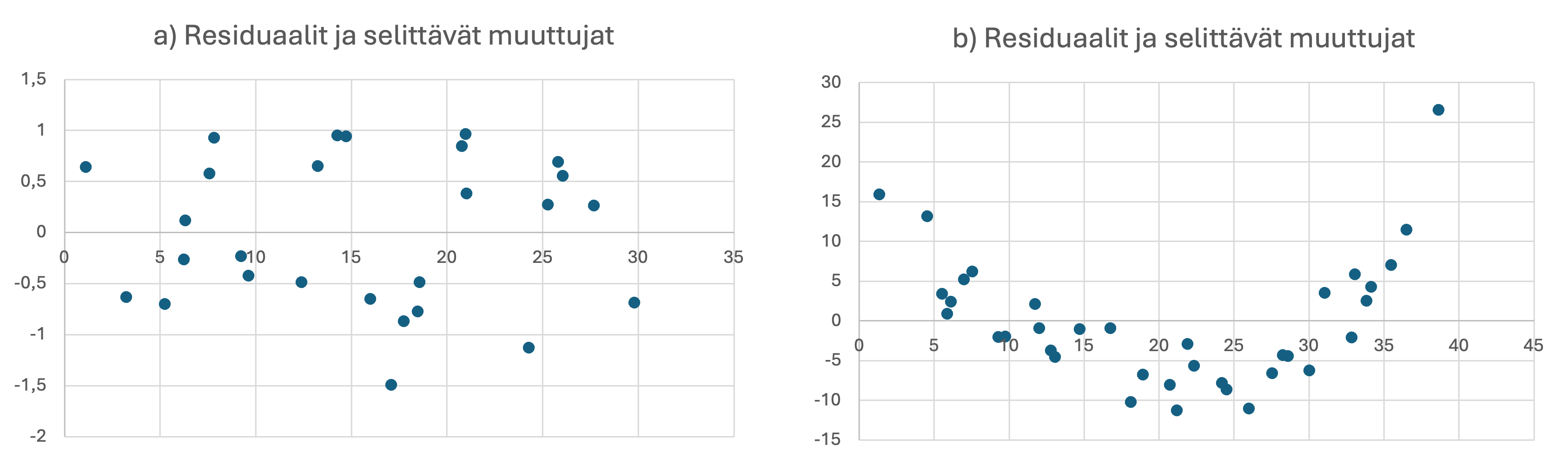
Figure 7.1: Kaksi residuaalikuvaa, joista kummastakin nähdään taustaoletusten paikkansapitämättömyys.
7.3.5.1 Durbin-Watson tunnusluku
Lineaarisen mallin taustalle tehtiin oletus residuaalien riippumattomuudesta ja siitä, että yhden residuaalin arvo ei vaikuta toisen residuaalin arvoon. Käytännön aineisto voi kuitenkin sisältää syklisyyttä, jota voidaan em. hajontakuvion ja visuaalisen tarkastelun lisäksi tarkastella ns. Durbin-Watson tunnusluvulla, joka määritellään seuraavasti \[D=\frac{\sum_{i=2}^n (e_i-e_{i-1})^2}{\sum_{i=1}^n e_i^2}.\] Mikäli perättäiset residuaalit ovat keskimäärin positiivisesti korreloituneet (positiivinen autokorrelaatio), niin suure \(D\) lähestyy arvoa nolla. Mikäli perättäiset residuaalit eivät ole peräkkäisesti korreloituneita (ei autokorrelaatiota), niin suure \(D\) lähestyy arvoa kaksi ja mikäli peräkkäiset residuaalit ovat keskimäärin negatiivisesti korreloituneet (negatiivinen autokorrelaatio), niin \(D\) on suurempi kuin kaksi ja lähestyy arvoa neljä. Durbin-Watson proseduurille on määritelty vastaavat havaintolukumääristä ja selittävien muuttujien lukumäärästä riippuvat kriittiset ala- ja ylärajat \(d_L\) ja \(d_U\), jotka löytyvät monista tilastollisista taulukoista (tai esim. täältä ). Näitä rajoja voidaan käyttää viiterajoina selvittämään ovatko residuaalit tilastollisesti riippumattomia. Jos siis esimerkiksi Durbin-Watson tunnusluku on valitulla luottamustasolla, havaintojen ja selittävien muuttujien lukumäärällä pienempi kuin taulukon kriittinen arvo \(d_l\) (tai suurempi kuin \(d_U\)), niin tästä voidaan päätellä, että residuaalit ovat positiivisesti (negatiivisesti) autokorreloituneet ja siten toisistaan riippuvia eikä lineaarisen mallin oletukset näin ollen pidä paikkaansa.
7.4 Testejä regressioparametreille
Edellä kuvattiin mallinsovitusta ja parametrien estimointia puhtaan matemaattisesti ilman mitään jakaumaoletuksia tai muuta satunnaisuutta. Seuraavassa tarkasteluun otetaan mukaan satunnaisuuden vaikutus havaitussa aineistossa ja estimoituja lineaarisen regression parametriarvoja tarkastellaan otossuureina, jotka on laskettu satunnaisuutta sisältävästä aineistosta. On selvää, että esimerkiksi pienellä otoskoolla ja suurella selittäjien kovariaattien määrällä satunnaisuuden vaikutus estimoituihin parametriarvoihin on suuri. Regressioparametreille on johdettu erilaisia testejä, joilla voidaan testata mallin sopivuutta ja tulosten merkitsevyyttä satunnaisuuden läsnäollessa. Tässä esitellään kaksi testiä
7.4.1 Yhteistesti parametreille
Koko lineaariselle regressiomallille voidaan tehdä yhteistesti, jossa testataan kerralla koko mallin tilastollista merkitsevyyttä regressioparametrien \(b_1,...,b_k\) kauttaTaustaoletus (yleinen hypoteesi): lineaarisen regression aiemmin määritellyt taustaoletukset ovat voimassa.
Testattava hypoteesi: testissä tutkitaan aineistoon perustuen ovatko kaikki regression kulmakertoimet eli muuttujen efektit samanaikaisesti nollia eli merkityksettömiä selittämään \(y\)-havaintoja
- \(H_0 : b_1 = b_2 = \cdots = b_k = 0\)
- \(H_1 : \text{ ainakin yksi }b_i \neq 0 , i\geq 1\)
Testisuure on muotoa \[F = \frac{(n-k-1)}{k}\frac{SSR}{SSE},\] jossa \(SSR= \sum_{i=1}^{n}(\hat{y}_i - \bar{y})^2\) ja \(SSE=\sum_{i=1}^{n}(y_i-\hat{y}_i)^{2}=\sum_{i=1}^{n}\epsilon_{i}^{2}\).
Näin määritellen \(F\sim F(k,n-k-1)\).
Testin taustalla on ajatus, että mikäli nollahypoteesi pätee, niin selittävät muuttujat eivät vaikuta ollenkaan selitettävän muuttujan arvoihin. Jos siis \(SSR\) on suuri suhteessa \(SSE\):hen, niin nollahypoteesi ei ole uskottava. Suuret testisuureen arvot puoltavat nollahypoteesin hylkäämistä, jolloin ainakin yksi selittäviin muuttujiin liittyvistä regressioparametreistä on nollasta poikkeava. Huomaa, että testissä tarkastellaan vain \(x\)-muuttujiin liittyviä kertoimia \(b_1,...,b_k\), mutta ei vakiotermiä \(b_0\).
7.4.2 Testi yksittäiselle regressioparametrille
Regressiomallin tiettyyn selittävään muuttujaan liittyvän regressioparametrin tilastollista merkitsevyyttä voidaan myös testata yksittäin
Taustaoletus (yleinen hypoteesi): lineaarisen regression aiemmin määritellyt taustaoletukset ovat voimassa.
Testattava hypoteesi: testissä tutkitaan aineistoon perustuen onko tietty regressioparametri \(b_j\) (jossa \(j=1,...,k\)) nolla eli merkityksetön selittämään \(y\)-havaintoja
- \(H_0 : b_j = 0\)
- \(H_1 : b_j \neq 0\)
Testisuure on muotoa \[t = \frac{b_j-0}{s_{b_j}},\] jossa \(s_{b_j}\) on regressioparametriin \(b_j\) liittyvä keskihajonta(estimaattori), joka on mittari efektin \(b_j\) satunnaisuudelle johtuen havaitun aineiston satunnaisuudesta.
Näin määritellen \(t\sim t(n-k-1)\).
Regressioparametrikohtaiset keskihajonnat \(s_{b_j}\) saadaan ottamalla neliöjuuret matriisin \(\hat{\sigma}^2(X^T X)^{-1}\) diagonaalielementeistä, jossa \(\hat{\sigma}^2\) on virhevarianssin \(\sigma^2\) estimaattori \[\hat{\sigma}^2 = \frac{SSE}{n-(k+1)}, \] joka kuvaa havaintopisteiden vaihtelua lasketun regressiomallin suhteen.
7.5 Lineaarisen mallin laajennuksia
Edellä kuvattua monen selittäjän lineaarista regressiota on mahdollista laajentaa eteenpäin monilla eri tavoilla. Alla on kuvattu muutamia laajennuksia
7.5.1 Indikaattori/dummy -muuttujan lisääminen malliin
Lineaariseen regressiomalliin on mahdollista lisätä mukaan binäärinen tai muuten luokiteltu selittävä muuttuja, joka on esimerkiksi indikaattori nominaalisesta muuttujasta. Binäärimuuttujan arvot on tämän osalta muotoa 0 (ei totta) tai 1 (totta). Tälle muuttujalle voidaan laskea aiemmin listatuin ehdoin (ei esimerkiksi multikollineaarisuutta) regressioparametrit, ja tällöin saatava parametri kertoo efektin voimakkuudesta, kun indikaattorimuuttuja on yksi.
7.5.2 Heteroskedastinen malli
Lineaarisessa regressiossa oletetaan tyypillisesti homoskedastinen virherakenne, eli \(Var(\epsilon_i)=vakio\). Tästä oletuksesta on mahdollista joustaa. Tällöin kuitenkin pienimmän neliösumman ratkaisu on hieman monimutkaisempi samoin kuin taustalla oleva teoria.
7.5.3 Korkeampiasteiset mallit
Mallin systemaattiseen osaan on mahdollista lisätä myös korkeampiasteisia selitystermejä, esimerkiksi neliöllisiä muuttujia \(x_i^2\) tai yhdysvaikutustermejä \(x_ix_j\) (\(i \neq j\)). Nämä voivat rikastaa mallia ja tekevät siitä huomattavasti joustavamman, mutta tekee mallinvalinnasta ja selittämisestä hankalampaa ja näitä laajennuksia on käytettävä ainoastaan hyvin harkitusti.
7.5.4 Moniulotteinen selitettävä ja moniulotteinen selittäjä
Yllä olevaa monen selittäjän lineaarista selitysmallia on mahdollista jatkaa tilanteeseen, jossa selitetään yksiulotteisen havainnon \(y_i\) sijasta moniulotteista havaintoa \(y_i\) moniulotteisella selittäjällä. Tällaista mallia kutsutaan suomenkielisessä kirjallisuudessa joskus nimellä moniulotteinen lineaarinen regressio ja englanninkielisessä kirjallisuudessa nimellä multivariate linear regression. Valitettavasti nämä termit menevät varsin usein sekaisin, sekä suomen että englannin kielessä, ja esimerkiksi termi “moniulotteinen regressio” tai “multivariate regression” tarkoittaa useimmille tilannetta, jossa yksiulotteista selitettävää muuttujaa mallinnetaan monen selittäjän lineaarisella - tai epälineaarisella - funktiolla. Tilanteen niin vaatiessa on hyvä aina selvittää mitä käytetyllä malliterminologialla tarkasti ottaen tarkoitetaan.
7.5.5 Satunnaisen havaintoaineiston asetelma (Random design regression)
Edellä tässä kappaleessa esitelty lineaarisen regression teoria perustui oletukseen kerätystä kiinteästä \((x,y)\) -havaintoaineistosta eli kyseessä on ns. kiinteän (havainto)asetelman tilanne (ns. fixed design regression). Regressiota on mahdollista tehdä myös tuleviin vielä havaitsemattomiin ja satunnaisiin havaintopareihin perustuen, jolloin kyseessä on satunnaisen asetelman tilanne (ns. random design regression).
7.5.6 Virheet selittäjissä (Errors in variables models)
Tyypillinen helpottava taustaoletus on, että selittävät muuttujat ovat kiinteitä ja ne oletetaan mitatuiksi virheettömästi. Lineaarisen regression teoriaa on mahdollista laajentaa myös tilanteeseen, jossa selittäville muuttujille oletetaan satunnaisuutta (ks. Errors in variables models).
